মুশফিকুর রহমান নিলয়

অ্যালগরিদমের টাইম কমপ্লেক্সিটি পর্ব ০৩

আমি আগেই বলেছিলাম অ্যালগরিদম ও ডেটা স্ট্রাকচার এর সব থেকে কঠিন পার্ট বলা হয় টাইম কমপ্লেক্সিটি কে। সুতরাং টাইম কমপ্লেক্সিটি টা খুব ভালো করে বুঝতে হবে। আর তোমাদের বুঝার সুবিধার জন্য টাইম কমপ্লেক্সিটিটা কে কয়েক টি পর্বে ভাগ করা হয়েছে।
প্রথম এবং দ্বিতীয় পর্বে টাইম কমপ্লেক্সিটির সম্পর্কে আইডিয়া দেওয়ার চেষ্টা করেছি এবং কিছু সমস্যার টাইম কমপ্লেক্সিটি ক্যালকুলেশন করেছি। অবশ্যই প্রথম পর্ব এবং দ্বিতীয় পর্ব বুঝে এই পর্বে আসতে হবে।

প্রথম পর্বে বলেছিলাম যে লাইন গুলা একবার মাত্র এক্সিকিউট হয় তার টাইম কমপ্লেক্সিটি হিসেব সাধারণত করা হয় না। যে কোড গুলো রিপিট হয়। মানে বার বার এক্সিকিউট হয় এমন লাইনের এক্সিকিউশন টাইম বের করতে হবে।
বার বার রিপিট হয় একমাত্র লুপ ব্যবহার করলে অথবা রিকার্শনের ক্ষেত্রে।

প্রথম এবং দ্বিতীয় পর্বে একটা সিঙ্গেল লুপের টাইম কমপ্লেক্সিটি কিভাবে বের করতে হয় সেটা শিখেছি। আজকে আমরা ইনার লুপের টাইম কমপ্লেক্সিটি বের করা শিখবো। মানে একটা লুপের মধ্যে আরেক টা লুপ।

উপরের প্রোগ্রামে ২টি আলাদা লুপ আছে। তুমি যদি প্রথম এবং দ্বিতীয় পর্ব বুঝে থাকো তাহলে খুব সহজেই লুপ ২টির টাইম কমপ্লেক্সিটি বলতে পারবে। আর যদি বুঝতে সমস্যা হয় তাহলে অবশ্যই আগের পর্ব গুলো দেখে তারপর এই পর্ব শুরু করা তোমার জন্য ভালো হবে।

লুপ ২টির টাইম কমপ্লেক্সিটি হচ্ছে O(n) এবং O(log2n + 1)।
যেহেতু ২টা টাইম কমপ্লেক্সিটি পেলাম সেহেতু ২টা টাইম কমপ্লেক্সিটি কে যোগ করে দিতে পারি O(n + log2n + 1)।
যদি এরকম আলাদা আলাদা লুপ থাকে তাহলে সব গুলা লুপের টাইম কমপ্ললেক্সিটি কে যোগ করে দিবো। এবং সেখান থেকে সব থেকে বড় সংখ্যা কে রাখতে পারি। অর্থাৎ O(n + log2n + 1) এখানে সব থেকে বড় হলো O(n)। সুতরাং আমরা সব গুলা দেখাতে পারি অথবা সব থেকে বড় সংখ্যাকেও দেখাতে পারি।

এখন একটু কঠিনের দিকে আসি। মানে এতক্ষণ আলাদা আলাদা লুপের টাইম কমপ্লেক্সিটি দেখেছি এখন একটা লুপের মধ্যে আরেক টা লুপের টাইম কমপ্লেক্সিটি দেখবো।

একটা লুপের মধ্যে আরেকটা লুপ থাকলে তাকে আমরা নেস্টেড লুপ বলি। সুতরাং এই নেস্টেড লুপের টাইম কমপ্লেক্সিটি কিভাবে বের করে?
উপরের প্রোগ্রামের প্রথম লুপটা দেখেই বুঝতে পারতেছি এর টাইম কমপ্লেক্সিটি O(n)। তাহলে ২য় লুপের টাইম টাইমপ্লেক্সিটি কত? ২য় লুপের টাইম টাইমপ্লেক্সিটিও O(n)।

প্রথম লুপে n এর মান ৫ এবং ২য় লুপের মান ৩ নিলাম। প্রথম লুপের i মান যখন ১ হবে তখন নেস্টেড লুপটা ৩ বার ঘুরবে। কারণ যতক্ষণ পর্যন্ত j এর মান মিথ্যা না হবে ততক্ষণ পর্যন্ত ঘুরবে। এভাবে প্রথম লুপটা ৫ বার ঘুরবে আর নেস্টেড লুপটা প্রতিবার ৩ বার করে ঘুরবে। তাহলে প্রথম লুপটা ঘুরবে ৫ বার অর্থাৎ টাইম কমপ্লেক্সিট হবে O(5), আর ২য় লুপেটা ঘুরবে ৩ বার করে ১৫ বার অর্থাৎ O(3)।
যদি ২টা টাইম কমপ্লেক্সিটিকে গুন করে দেই O(3X5) তাহলে রেজাল্ট হলো O(15)।

তুমি যদি উপরের প্রোগ্রামে ৫ এবং ৩ বসিয়ে লুপটা চালাও তাহলে দেখবে "Time Complexity" লিখাটা ১৫ বার প্রিন্ট হবে।
আর যদি n বসিয়ে হিসেব করো তাহলে O(n x n), অর্থাৎ O(n2) হবে।

এতক্ষণ পর্যন্ত যদি সব কিছু বুঝে থাকো, তাহলে নিচের প্রোগ্রামের টাইম কমপ্লেক্সিটি নিজে নিজে বের করার চেষ্টা করো।

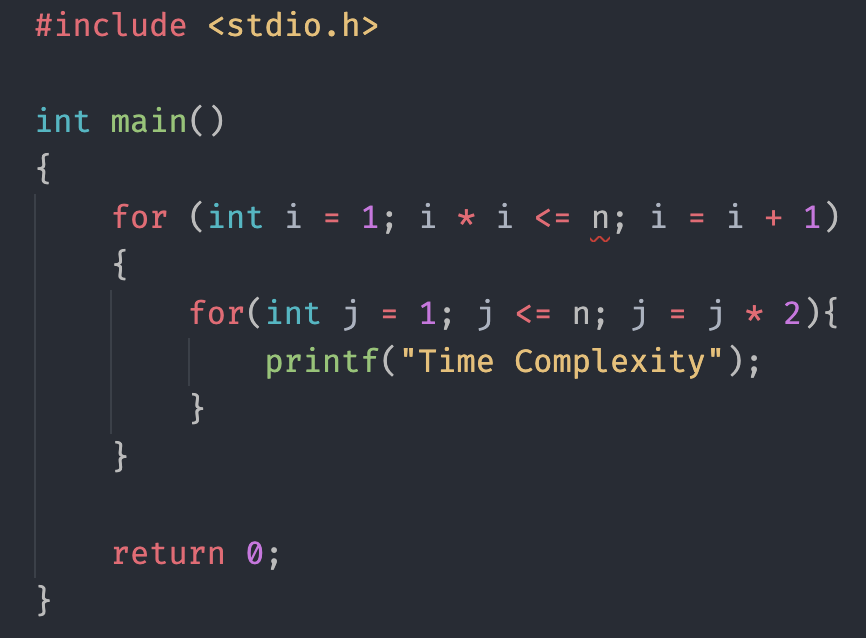
উপরের প্রোগ্রামের টাইম কমপ্লেক্সিটি হবে । যদি তোমার রেজাল্টের সাথে আমার রেজাল্ট মিলে যায়, তাহলে তোমাকে অভিনন্দন। কারণ তুমি নিজে চেষ্টা করে টাইম কমপ্লেক্সিটি বের করতে সক্ষম হয়েছো। আর যদি চেষ্টা করেছো কিন্তু রেজাল্ট মিলে নি, তাহলেও তোমাকে অভিনন্দন। আর যারা ব্যর্থ হয়েছো, তাদের কে বলবো আগের পর্ব গুলো আরো ভালো মত পড়তে।
কারণ প্রথম লুপের টাইম কমপ্লেক্সিটি আমরা প্রথম পর্বে শিখে এসেইছিলাম। এর টাইম কমপ্লেক্সিটি হবে O(√n)।
আর দ্বিতীয় অর্থাৎ নেস্টেড লুপের টাইম কমপ্লেক্সিটি হবে O(log2n + 1)।
এখন ২টা টাইম কমপ্লেক্সিটি কে যদি গুন করে দেই O(√n * log2n + 1)।

যদি এরকম ৩ টা নেস্টেড লুপ থাকত তাহলে ৩টা লুপের আলাদা আলাদা টাইম কমপ্লেক্সিটি বের করে গুন করে দিব।

আচ্ছা বলত নিচের প্রোগ্রামের টাইম কমপ্লেক্সিটি কত হবে?

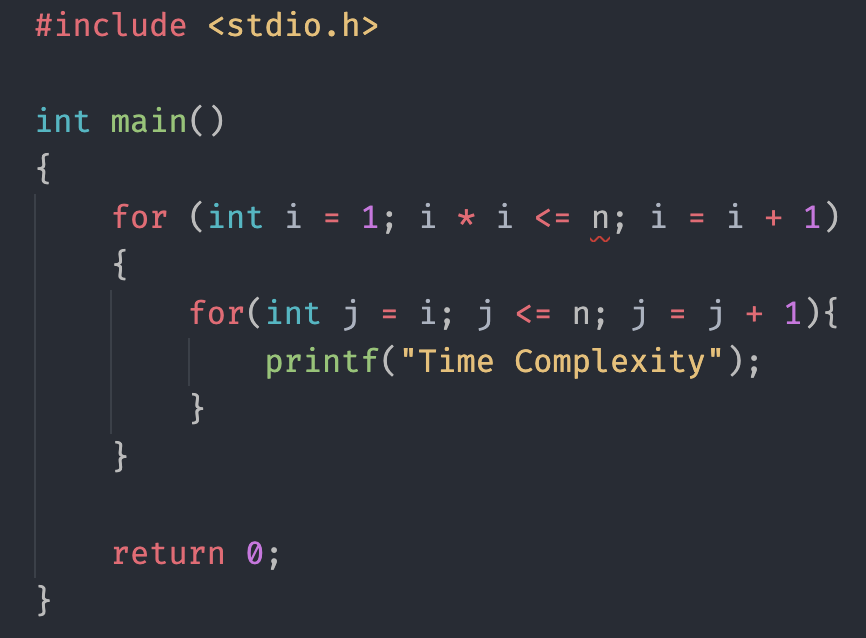
ভালো মত লক্ষ করে দেখো নেস্টেড লুপের j এর মান কিন্তু i এর মানের উপর নির্ভর করছে। সুতরাং নেস্টেড লুপটা কতবার ঘুরবে সেটা নির্ভর করবে i এর মান কত। নিচের ছবিটা দেখে বুঝার চেষ্টা করো।

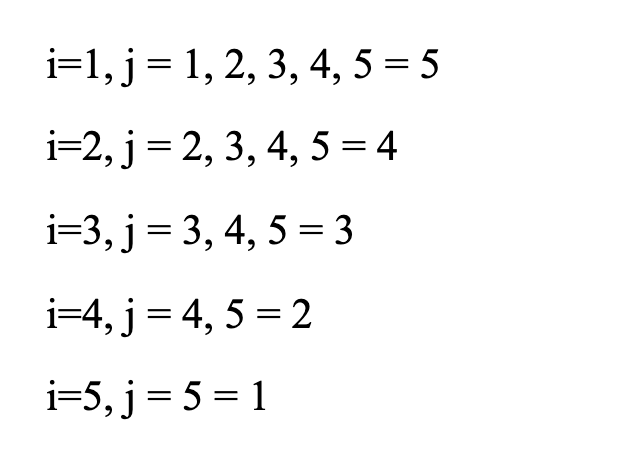
এখানে প্রথম লুপ এবং নেস্টেড লুপের n এর মান ৫ বসিয়েছি। যখন i এর মান ১ তখন নেস্টেড লুপটা ৫ বার ঘুরছে। আর যখন i এর মান ২ তখন নেস্টেড লুপটা কিন্তু ২ থেকে ঘুরা শুরু হবে। কারণ নেস্টেড লুপে বলা আছে j = i অর্থাৎ i এর মান যদি হয় ২ তাহলে j এর মান হবে ২। তাহলে ২ থেকে নেস্টেড লুপ টা ঘুরা শুরু করবে।

এটার রেজাল্ট আসবে এরকম 1 + 2 + 3 + 4 + 5। আমরা n এর মান ৫ বসিয়েছি তাই ৫ পর্যন্ত। যদি ১০০ বসাতাম তাহলে ১০০ পর্যন্ত হত। আর যদি n বসাই তাহলে 1 + 2 + 3 + 4 + ...... + n
তাহলে 1 থেকে n এর যোগফলের সূত্র হচ্ছে n*(n+1)/2

উপরের প্রোগ্রামের টাইম কমপ্লেক্সিটি হবে O(n*(n+1)/2)। এটাকে যদি আরো ভেঙ্গে লিখি তাহলে O((n2+n)/2)।
আমরা জানি নরমাল কোন ছোট সংখ্যা দ্বারা যদি ভাগ হয় তাহলে সেই সংখ্যাটা কে বাদ দিতে পারি O(n2+n)। এবং এখানে সব থেকে বড় সংখ্যাটা কে রাখবো। সেটা হলো O(n2)। O(n2) হলো উপরের প্রোগামের টাইম কমপ্লেক্সিটি।
তুমি চাইলে O(n*(n+1)/2) এই প্রোগ্রামের টাইম কমপ্লেক্সিটি বলতে পারো।