মুশফিকুর রহমান নিলয়

অ্যালগরিদমের টাইম কমপ্লেক্সিটি পর্ব ০১

অ্যালগরিদম ও ডেটা স্ট্রাকচার এর সব থেকে কঠিন পার্ট বলা হয় টাইম কমপ্লেক্সিটি কে। কারণ তোমরা জানো একটা নিদিষ্ট সমস্যার জন্য একাধিক সমাধান থাকতে পারে। এর জন্য আমাদের খুঁজে বের করতে হবে কোন সমাধানটা স্মার্ট এবং কম সময়ে সঠিক রেজাল্ট দিবে।স্মার্ট সমাধানের জন্য আমাদের টাইম কমপ্লেক্সিটি সম্পর্কে ভালো ধারনা থাকতে হবে।
এই পর্বে টাইম কমপ্লেক্সিটির বেসিক একটা ধারনা নিবো এবং দ্বিতীয় পর্বে এডভান্স টাইম কমপ্লেক্সিটি শিখবো।

টাইম কমপ্লেক্সিটি বলতে একটা প্রোগ্রাম চলতে কতক্ষণ সময় নিবে। অর্থাৎ আপনি একটা সমস্যা সমাধান করেছেন, সেই সমাধানের প্রোগ্রামটা রান করতে কতক্ষণ সময় নিচ্ছে।

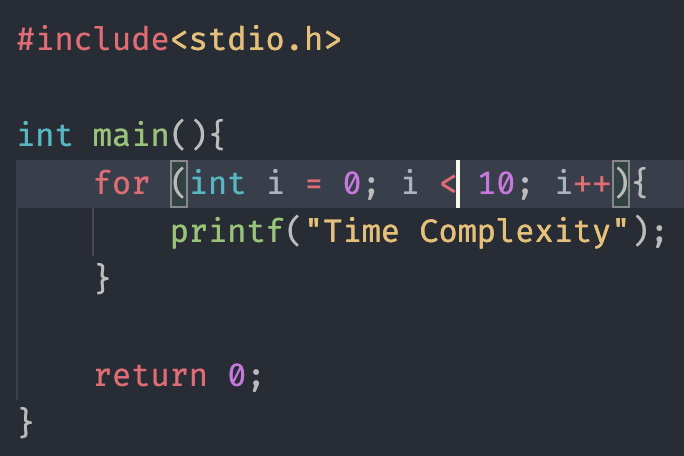
উপরের প্রোগ্রাম টা মোট কতবার “Time Complexity” লেখাটা প্রিন্ট করবে? প্রোগ্রামিং এর বেসিক নলেজ থাকলেই যে কেউ বলতে পারবে ১০ বার প্রিন্ট হবে। কারণ ফর লুপটা ১০ বার ঘুরতেছে।
এখন যদি বলা হয় এই প্রোগ্রামে সর্বোমোট কতটি লাইন এক্সিকিউট হবে? নিচের ছবিটা দেখে বুঝার চেষ্টা করুন।

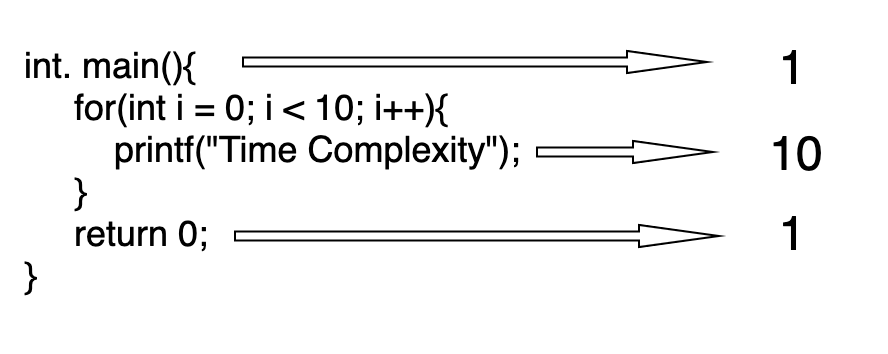
উপরের প্রোগ্রামটি সর্বোমোট ১২ টি লাইন এক্সিকিউট হবে।
সুতরাং একটা প্রোগ্রামে কতটা লাইন এক্সিকিউট করবে সেটাই বের করতে হবে এবং তার উপর বেস করে টাইম কমপ্লেক্সিটি বের করতে হবে।

যদি কোন একটা প্রোগ্রামে 10^8 সংখ্যাক লাইন এক্সিকিউট হয় তাহলে সি ল্যাঙ্গুয়েজে ১ সেকেন্ড সময় নেয়। অন্যান্য প্রোগ্রামিং ল্যাঙ্গুয়েজে কম বেশি লাগতে পারে।
এখন আপনাদের জন্য ছোট একটা প্রশ্ন হলো 10^8 সংখ্যাক লাইন এক্সিকিউট করতে যদি ১ সেকেন্ড সময় নেয়, তাহলে 10^12 সংখ্যাক লাইন এক্সিকিউট করতে কতক্ষণ সময় নিবে?

এর উত্তর হচ্ছে 166.66 মিনিট।
এখন হয়ত অবাক হয়ে চিন্তা করবেন মাত্র Power 4 এর জন্য এত পার্থক্য?
মনে করেন 10^1 কলমের দাম 10 টাকা। তাহলে 10^2 কলমের দাম আসতেছে 100 টাকা, 10^3 কলমের দাম আসতেছে ১,০০০ টাকা, আর 10^4 কলমের দাম আসতেছে 10,000 টাকা। আশা করি বুঝতে পারছেন।

তাহলে ফর লুপের মধ্যে ১০ উল্লেখ করে দেওয়াতে “Time Complexity” লেখাটা ১০ বার প্রিন্ট হয়েছে। যদি লুপে ১০০ উল্লেখ করে দেই তাহলে ১০০ বার প্রিন্ট হবে। যদি লুপে এক লক্ষ উল্লেখ করে দেই তাহলে এক লক্ষ বার প্রিন্ট হবে। এটা একটা সহজ হিসেব।

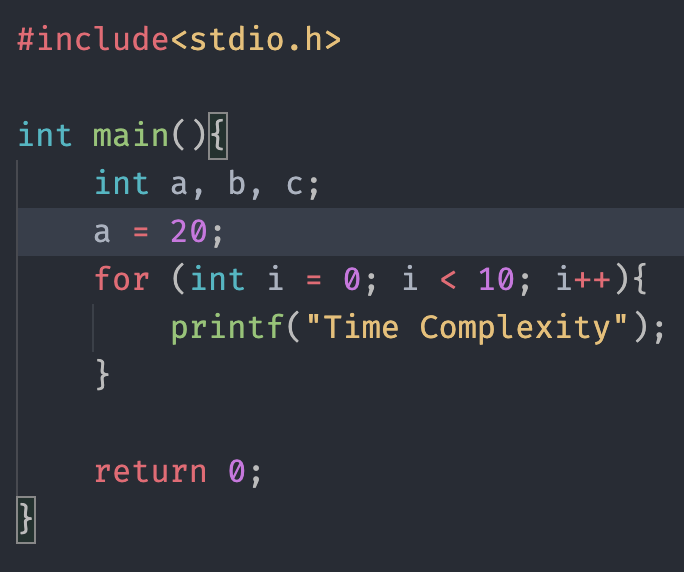
আগের প্রোগ্রামটার সাথে আরো ২ টা লাইন নতুন করে যোগ করেছি। লক্ষ করুন এখানে a, b & c নামে আলদা ৩ টা ভেরিয়েবল নিলেও ৩ বার এক্সিকিউট হবে না। এক্সিকিউট হবে ১ বার। a = 20; এটি একটি আলাদা লাইন তাই এটা ১ বার এক্সিকিউট হবে।

১। এস্যাইনমেন্ট অপারেশন
২। কম্পারিজন অপারেশন
৩। গাণিতিক অপারেশন
৪। ফাংশন কল
উপরের ৪ টা ছাড়া আরো কিছু অপারেশন আছে, যেগুলা সাধারণত ১ বার করে এক্সিকিউট হয়ে থাকে।

যখন একটা লাইন এক্সিকিউট হয়, তখন তাকে চিহ্নিত করা হয় O(1) দিয়ে। O() এটাকে (Big O Notation) বলা হয়।
যদি ১০ টা লাইন এক্সিকিউট হয় তাহলে O(10) অথবা ১০০ টা লাইন এক্সিকিউট হলে O(100) বলা হয়।
যে লাইন গুলা একবার মাত্র এক্সিকিউট হয় তার টাইম কমপ্লেক্সিটি হিসেব সাধারণত করা হয় না।

এখন হয়ত একটু অভাক হবেন, যদি সিঙ্গেল লাইনের এক্সিকিউশন টাইম বাদ দেই তাহলে কোন লাইন গুলোর টাইম কমপ্লেক্সিটি বের করবো বা করে?
উত্তর হচ্ছে, যে কোড গুলো রিপিট হয়। মানে বার বার এক্সিকিউট হয় এমন লাইনের এক্সিকিউশন টাইম বের করতে হবে।
বার বার রিপিট হয় একমাত্র লুপ ব্যবহার করলে অথবা রিকার্শনের ক্ষেত্রে।

মনে করেন আপনার একটা প্রোগ্রাম আছে ৫০ লাইনের। প্রতিটা লাইন একবার করে এক্সিকিউট হয়। তাহলে এর টাইম কমপ্লেক্সিটি হবে O(50)। এটা সহজ হিসেব। কিন্তু সমস্যাটা হয় যখন একই কাজ বার বার করতে হয়। এবং তখনই টাইম কমপ্লেক্সিটি নিয়ে সমস্যায় পড়ে যাই।

উপরের প্রোগামটা দেখে আমরা সহজেই বুঝতে পারি “Time Complexity” ১০ বার প্রিন্ট করবে। এবং এর টাইম কমপ্লেক্সিট বলতে পারি O(10)। কিন্তু লুপে যদি ৫০ অথবা ৫০০ সেট করে দেই, তাহলে এর টাইম কমপ্লেক্সিটি হবে O(50) অথবা O(500)।

তাহলে লুপের মধ্যে ভ্যালুটা চেঞ্জ হলে টাইম কমপ্লেক্সিটিও চেঞ্জ হচ্ছে। লুপের ভ্যালু ইউজারের উপর নির্ভর করতেছে। সুতরাং লুপটা n সংখ্যাক বার চলতে পারে। তাই তাকে O(n) Big O n or Order of n বলা হয়। যদিও লুপে একটা মাত্র লাইন কিন্তু প্রিন্ট হবে n সংখ্যাক বার।

এখানে একটা ব্যাপার বলে রাখি লুপের কন্ডিশন যতক্ষণ সত্য হবে ততক্ষণ লুপটা চলবে। কিন্তু লুপের কন্ডিশন মিথ্যা হওয়ার জন্য অতিরিক্ত একবার ঘুরবে। অর্থাৎ O(n + 1) বার ঘুরবে। কিন্তু টাইম কমপ্লেক্সিটির ক্ষেত্রে কনস্টেন্ট হিসেব করা হয় না। তাই শুধু O(n) হিসেব করা হয়।

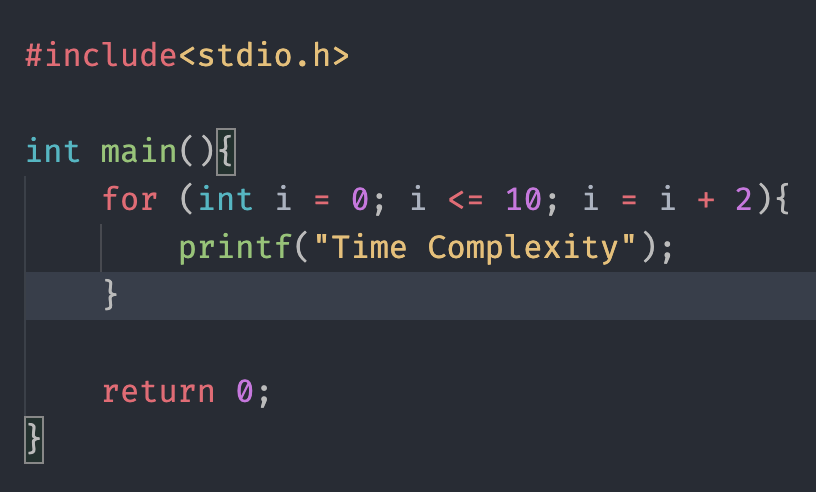
এই লুপটি লক্ষ্য করুন, এখানে i এর মান প্রতিবার ২ করে বাড়ছে। তাহলে ১০ এর জন্য মোট ৫ বার লুপটি ঘুরবে। আর যদি ২০ দেওয়া হয়? তাহলে ১০ বার ঘুরবে। তাহলে টাইম কমপ্লেক্সিটি বলা যায় O(10/2) or O(20/2)। আর n সংখ্যাক বার লুপটি ঘুরলে O(n/2)।

উপরের হিসেব যদি বুঝে থাকেন তাহলে নিচের লুপটি কতবার ঘুরবে?

এখানে i এর মান প্রতিবার ১ করে বাড়ছে, কিন্তু কন্ডিশন চেক করছে i * i করে। তাহলে ৩৬ এর মধ্যে কতবার লুপটি ঘুরবে? নিচে লুপের ক্যালকুলেশন করে দেওয়া হলো।

৩৬ এর জন্য ৬ বার ঘুরতেছে। যদি ৪৯ থাকত তাহলে ৭ বার ঘুরত আর যদি ২৫ থাকত তাহলে ৫ ঘুরত। তার মানে যে ভ্যালুটাকে যদি root করে দেই তাহলেই হলো।
যদি n সংখ্যাক ভ্যালু থাকে তাহলে টাইম কমপ্লেক্সিটি হবে O(√n)

আজকের পর্বে এই পর্যন্তই। পরের পর্বে টাইম কমপ্লেক্সিটিটির আরো গুরুত্বপুর্ণ টপিক সম্পর্কে জানবো।
যেমন Best Case, Average case & Worst Case এবং Space Complexity সম্পর্কে জানবো।