মুশফিকুর রহমান নিলয়

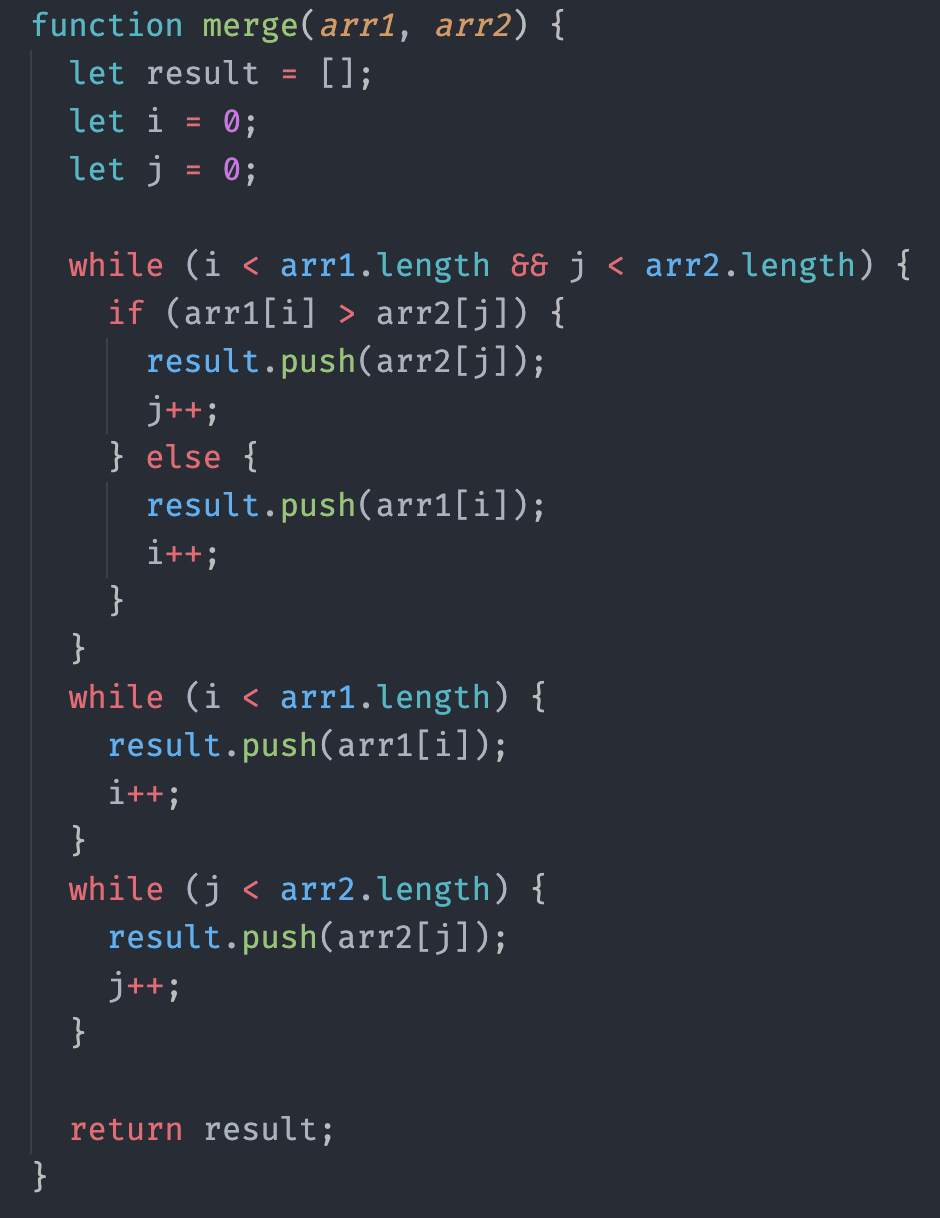
মার্জ সর্ট অ্যালগরিদম

সর্টিং অ্যালগরিদম গুলোর মধ্যে খুবই জনপ্রিয় একটু অ্যালগরিদম হলো মার্জ সর্ট অ্যালগরিদম। আজকে আমরা মার্জ সর্ট এর অ্যালগরিদম নিজ হাতে লিখবো, কোড করবো এবং মার্জ সর্ট অ্যালগরিদম এর টাইম কমপ্লেক্সিটি বের করার চেষ্টা করবো। সুতরাং ধৈর্য নিয়ে পড়তে হবে।

মার্জ সর্ট অ্যালগরিদম জানার আগে আমাদের আরেকটা বিষয় জানতে হবে, আর তা হচ্ছে ডিভাইড এন্ড কনকার। কারণ মার্জ সর্ট হলো ডিভাইড এন্ড কনকার এর একটি অ্যালগরিদম। এখন প্রশ্ন হলো ডিভাইড এন্ড কনকার কি?

মনে করো তোমাকে একটা বড় সমস্যা দেওয়া হলো, এখন তুমি সেই বড় সমস্যা কে ছোট ছোট অনেক গুলো ভাগে বিভক্ত করলে। নিচের ছবির মত

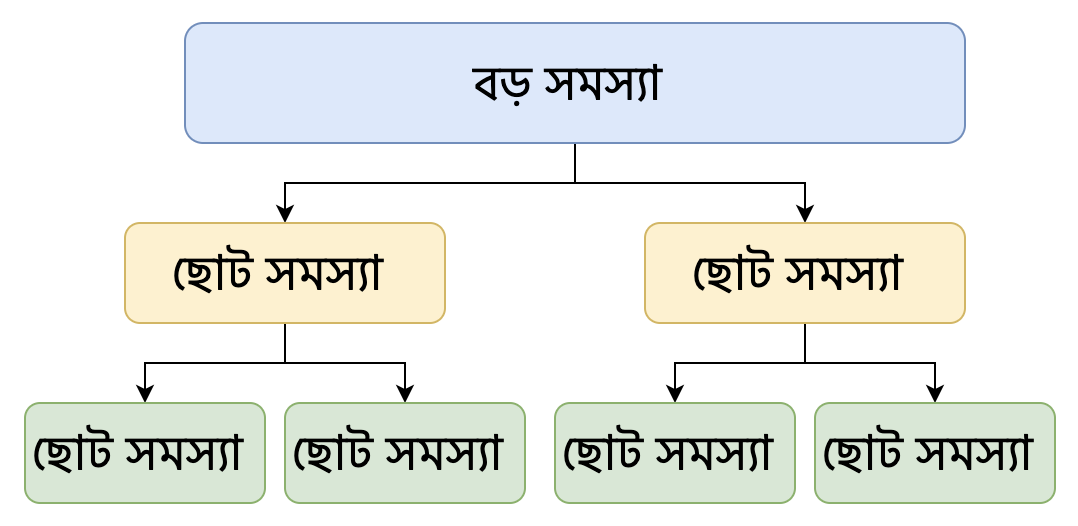
তুমি চাইলে ছোট সমস্যা গুলো কে আরো কয়েক টি ভাগে বিভক্ত করতে পারো। অর্থাৎ একটা বড় সমস্যা কে নিজেদের প্রয়োজন মত অনেক গুলা ভাগে বিভক্ত করা যায়। এখানে নিদিষ্ট কোন সীমাবদ্ধ নেই। উপরের ছবিতে দেখো একটা বড় সমস্যা কে প্রথমে ২ টি ভাগে বিভক্ত করা হয়েছে। তারপর সেই ২ টি ছোট সমস্যা কে আরো ছোট আকারে বিভক্ত করা হয়েছে।

ছোট ছোট সমস্যা গুলো কে বলা হয় Sub Problem অর্থাৎ একটা বড় সমস্যার অনেক গুলো ছোট সমস্যা(sub problem) পাবো যেই ছোট সমস্যা গুলো সমাধান করে বড় সমস্যার সমাধান পাবো।

ছোটবেলায় তোমরা সরল অংক করেছো নিশ্চয়ই। করলে হয়ত তেমন মনে নেই। মনে করিয়ে দেওয়ার জন্য নিচে ছোট একটা সরল অংক করলাম।

দেখো প্রথমে (1+4) যোগ করা হইছে, তারপর (4*6) এতটুকু অংশের কাজ করা হইছে। তারপর 5/5 ভাগ করে তার পরের লাইনে 1-24 বিয়োগ করে আমরা ফাইনাল রেজাল্ট পেয়েছি। এই টেকনিক টাই ব্যবহার করা হয়েছে ডিভাইড এন্ড কনকার অ্যালগরিদমে।

এখন এই ডিভাইড এন্ড কনকার এর বেশ কিছু অ্যালগরিদম আছে। যেমন মার্জ সর্ট, কুইক সর্ট সহ আরো কিছু অ্যালগরিদম আছে।

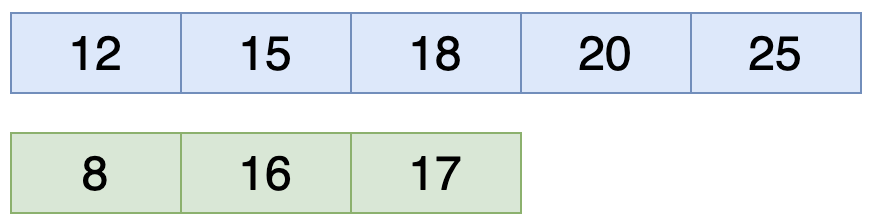
উপরের ছবিটা একটু ভালো করে লক্ষ্য করে দেখো এখানে ২ টা Array নেওয়া হয়েছে। এবং Array ২ টা Ascending Order এ সর্টেড করা। তুমি যদি এলোমেলো করে নাও অথবা Descending Order এ নাও তা হলে কিন্তু হবে না।

এখন এই Array 2 টা কে একত্রে করে Ascending Order সাজাতে হবে। তোমার মাথায় হয়ত চট করে আইডিয়া আসবে যে প্রথমে ২ টা Array কে connect করতে হবে তারপর বাবল সর্ট অ্যালগরিদম চালিয়ে দিলেই ত হয়ে যাচ্ছে। নিচের ছবির মত।

তোমরা আগের পর্বে বাবল সর্ট অ্যালগরিদম শিখেছ সুতরাং বাবল সর্ট অ্যালগরিদম ব্যবহার করলে আমারা রেজাল্ট পাবো কিন্তু সমস্যা হচ্ছে বাবল সর্ট অ্যালগরিদমের টাইম কমপ্লেক্সিটি O(n2)। এই টাইম কমপ্লেক্সিটি কে কমানো যায় কিনা সেই চেষ্টা করবো।

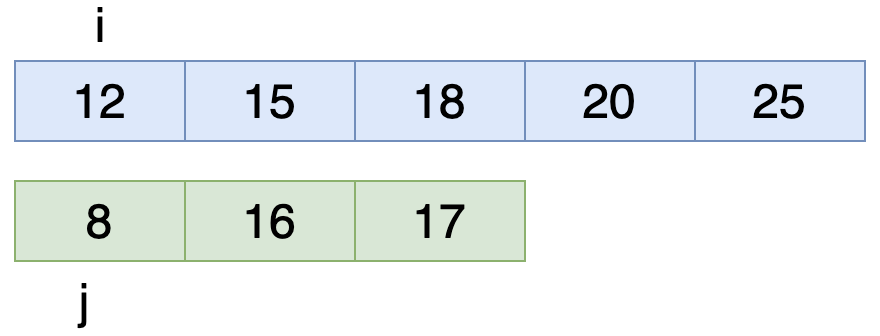
প্রথম Array এর প্রথম ইনডেক্স টা কে ধরলাম i এবং দ্বিতীয় Array এর ইনডেক্স টা কে ধরলাম j দিয়ে। তুমি চাইলে i এবং j এর জায়গায় যে কোন কিছু ব্যবহার করতে পারো।
এখন i এবং j এর ভ্যালুর মধ্যে চেক করবো কোন টা ছোট। যেহেতু 8 ছোট তাই আরেক টা Array তে আমরা এই ভ্যালুকে রাখবো। নিচের ছবিটা দেখো

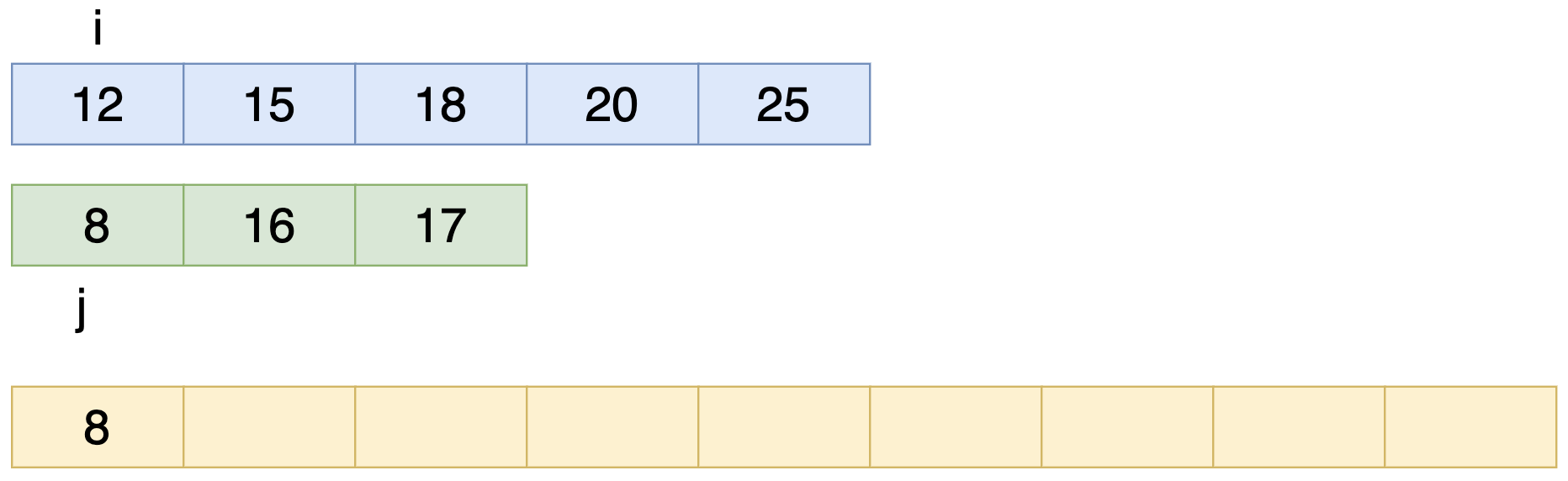
নতুন একটা Array তে j এর ভ্যালু কে রাখলাম যেহেতু j এর ভ্যালু ছোট। তাহলে j এর পজিশন অর্থাৎ ইনডেক্স চেঞ্জ হবে। নিচের ছবিটা দেখো

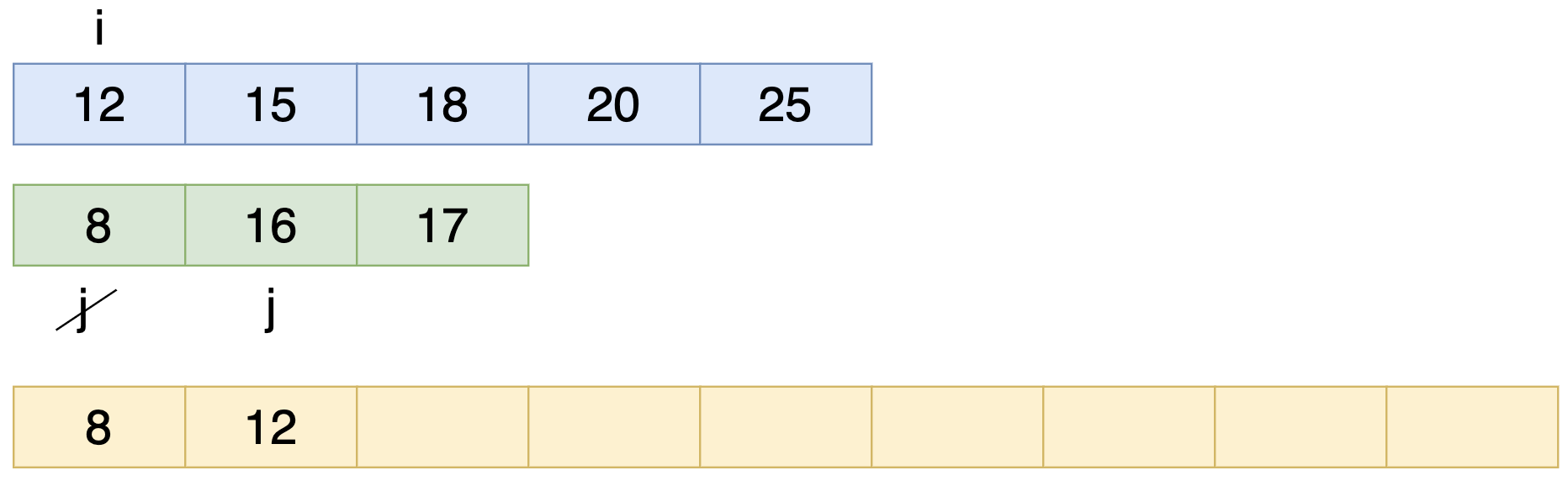
i এবং j এর ভ্যালুর মধ্যে চেক করবো কোন টা ছোট। যেহেতু i এর ভ্যালু 12 ছোট তাই i এর ভ্যালু কে নতুন Array তে রাখলাম।

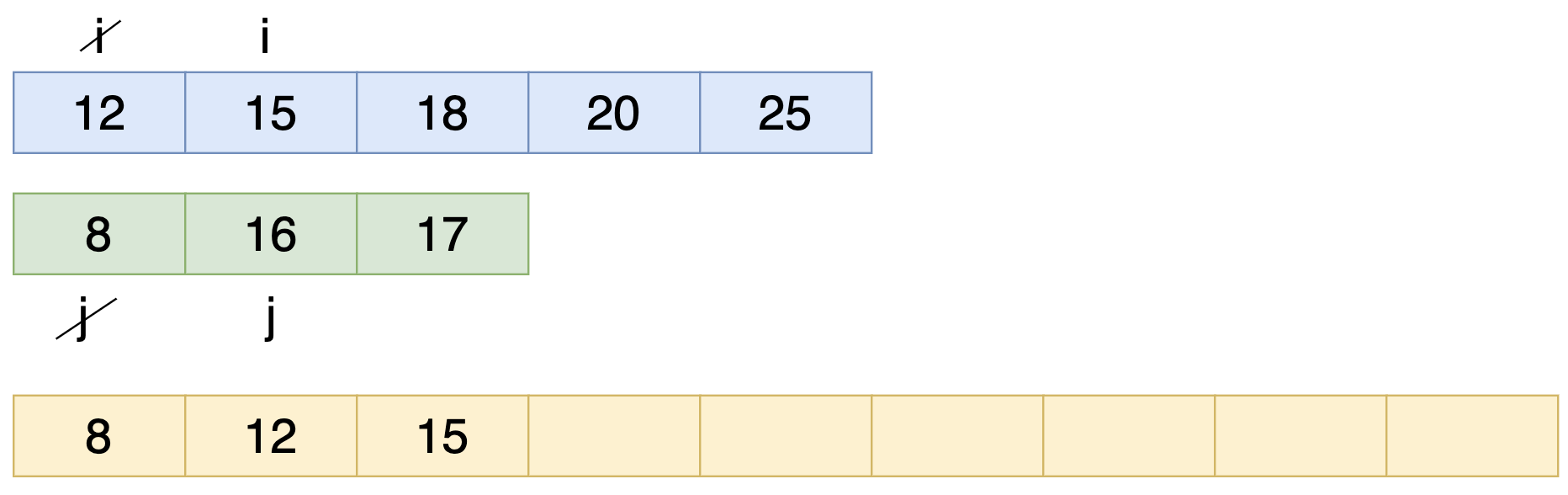
এখন i এর পজিশন চেঞ্জ হবে। এবং i এবং j এর ভ্যালুর মধ্যে চেক করবো কোন টা ছোট। যেহেতু i এর ভ্যালু 15 ছোট তাই i এর ভ্যালু কে নতুন Array তে রাখলাম।

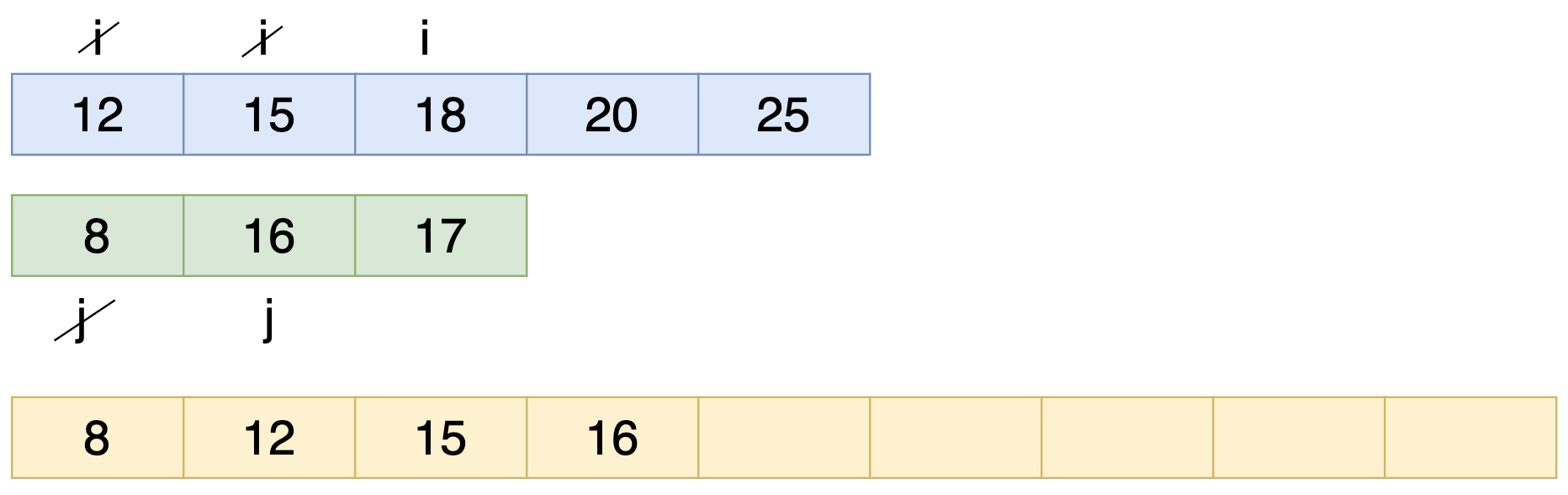
যেহেতু j এর ভ্যালু 16 ছোট তাই j এর ভ্যালু কে নতুন Array তে রাখলাম।

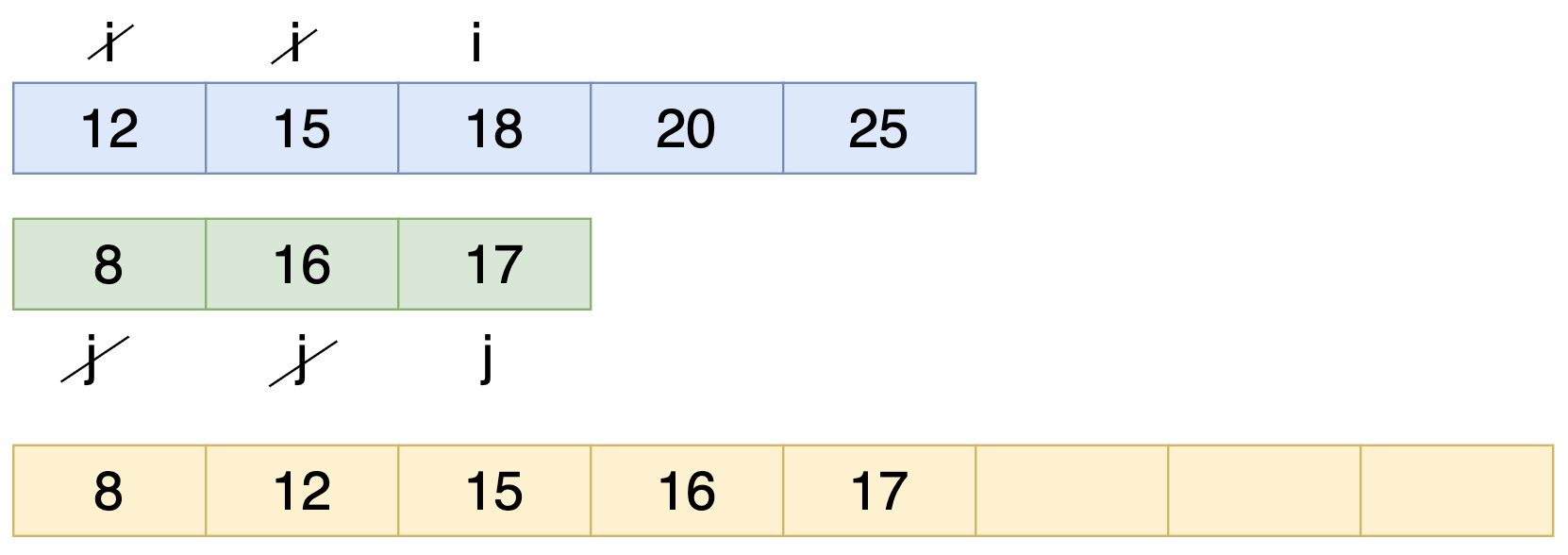
যেহেতু j এর ভ্যালু 17 ছোট তাই j এর ভ্যালু কে নতুন Array তে রাখলাম।
এখন কিন্তু দ্বিতীয় Array এর ভ্যালু শেষ সুতরাং প্রথম Array অর্থাৎ i এর ভ্যালু গুলো বসে যাবে। নিচের ছবি টা দেখো

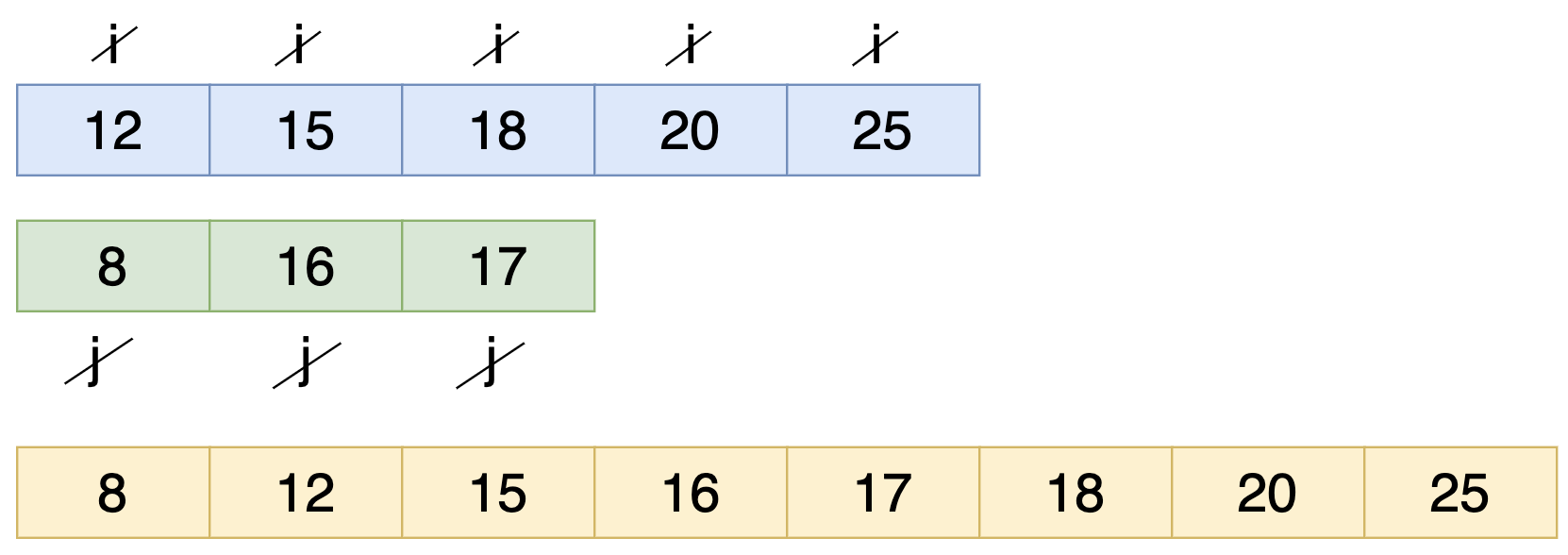
আমরা কিন্তু Ascending Order এ সর্টেড করে ফেললাম।

এখানে টাইম কমপ্লেক্সিটি কত লাগছে? O(n) কারণ আমরা একবার করে চেক করতেছি। যেহেতু এখানে টোটাল 8 টা এলিমেন্ট তাই O(8) হবে। যেখানে বাবল সর্ট অ্যালগরিদম ব্যবহার করলে টাইম কমপ্লেক্সিটি হত O(n2) অর্থাৎ O(82) = O(64)।

এখন আমরা মার্জ সর্ট অ্যালগরিদমে ফিরে আসি।

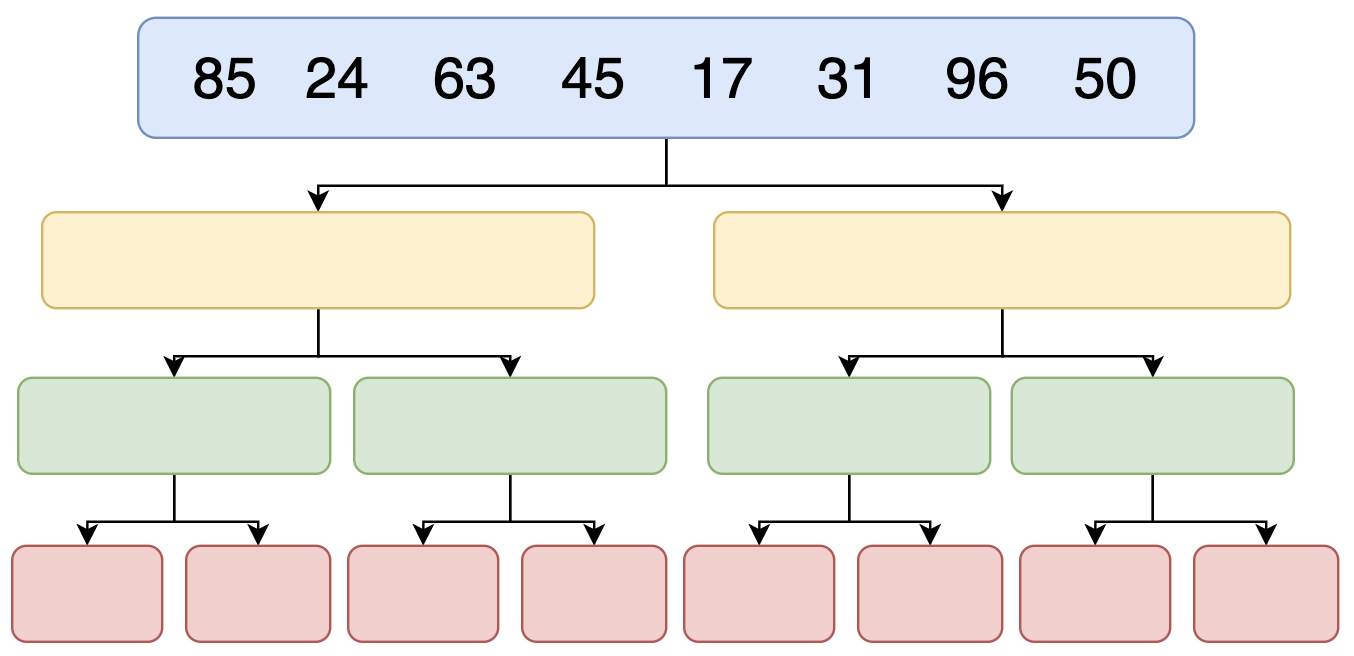
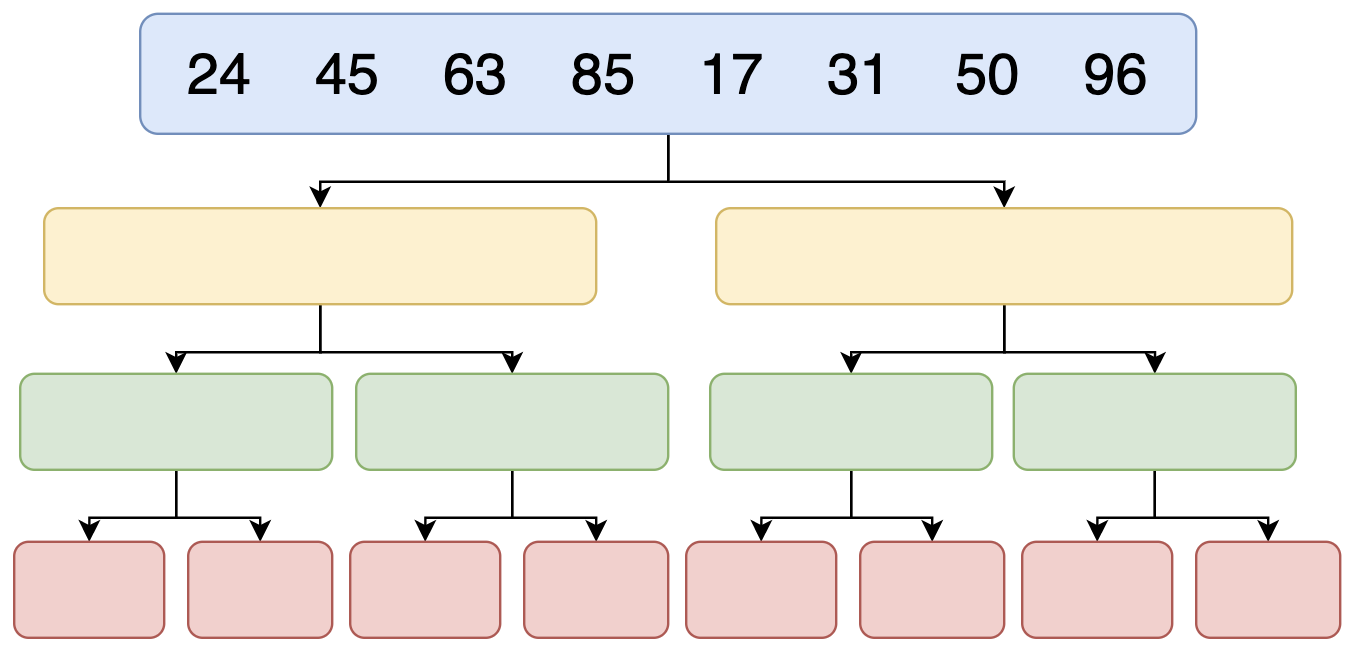
উপরের ছবিটা লক্ষ্য করে দেখো এখানে একটা Array আছে যেখানে ৮ টা এলিমেন্ট আছে। আমাদের কাজ হচ্ছে Ascending Order এ সাজানো। ডিভাইড এন্ড কনকার এ বলেছিলাম একটা বড় সমস্যা(Array) কে ছোট ছোট ভাগে বিভক্ত করে তা সমাধান করা।
বলে রাখা ভালো যে তোমাকে যে Array টা দেওয়া হবে সেটা কে ভেঙ্গে ভেঙ্গে একবারে একটা এলিমেন্টে নিয়ে আসতে হবে। এটা হচ্ছে মার্জ সর্ট অ্যালগরিদমের প্রথম টার্গেট। Array প্রতিটা এলিমেন্টকে আলাদা আলাদা করে ফেলা।
এখন উপরের ছবিতে একটা Array আছে যেটাকে Ascending Order সাজাতে হবে। তুমি চাইলে Descending Order ও সাজাতে পারো।

প্রথমেই Aarry টাকে দুই ভাগে ভাগ করবো। নিচের ছবির মত

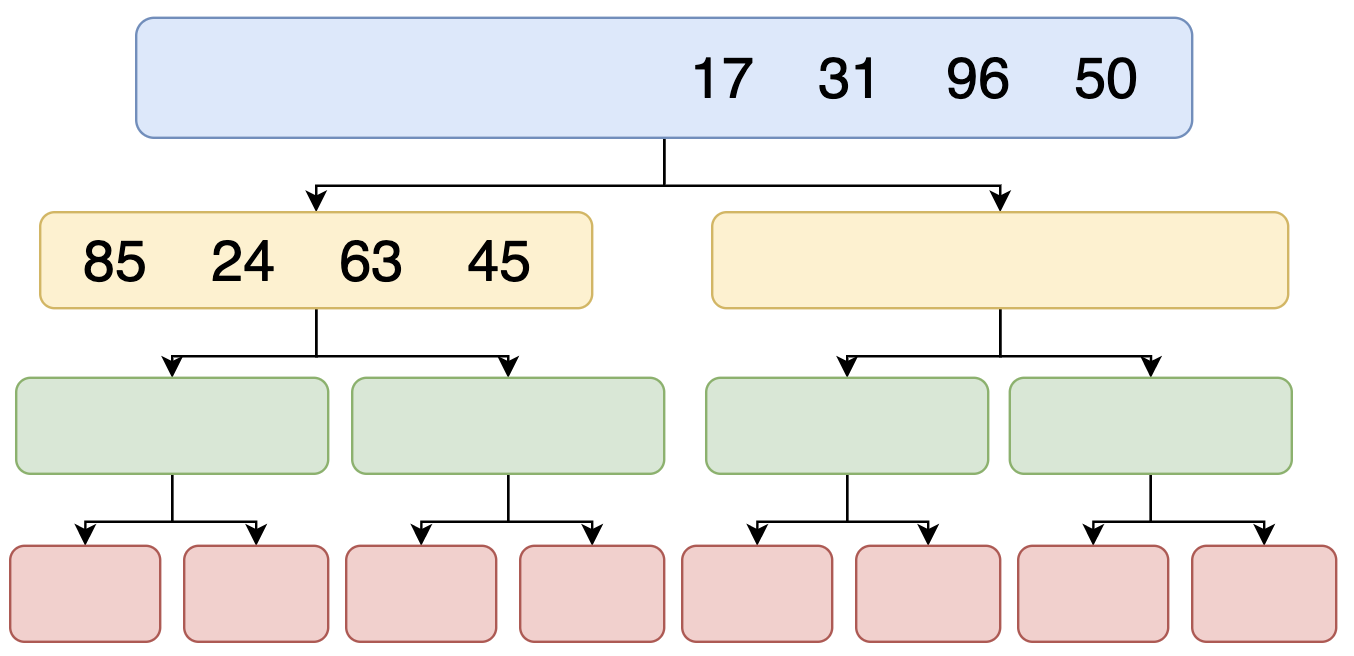
সব সময় সে মাঝ বরাবর দুই ভাগে ভাগ করবে। এখন প্রশ্ন হলো যদি ৯ টা এলিমেন্ট থাকে? যদি বিজোড় এলিমেন্ট থাকে তাহলে হয়ত সে প্রথম ভাগে ৪ টা নিবে পরের ভাগে ৫ টা নিবে অথবা প্রথম ভাগে ৫ টা পরের ভাগে ৪ টা নিতে পারে। তবে ব্যাপার টা হচ্ছে ১ টার বেশি পার্থক্য থাকবে না। আর সেটা নিয়ে আমাদের তেমন চিন্তা না করলে হবে। শুধু এতটুকু মাথায় রাখো যে সে মাঝ বরাবর দুই ভাগ করবে।
বাম পাশের অংশ টুকুর কাজ সে আগে করবে। কারণ কম্পিউটার প্রথমে একটা অংশের কাজ করে। এখন ডান পাশের অংশ টুকু আগে করতে পারে।

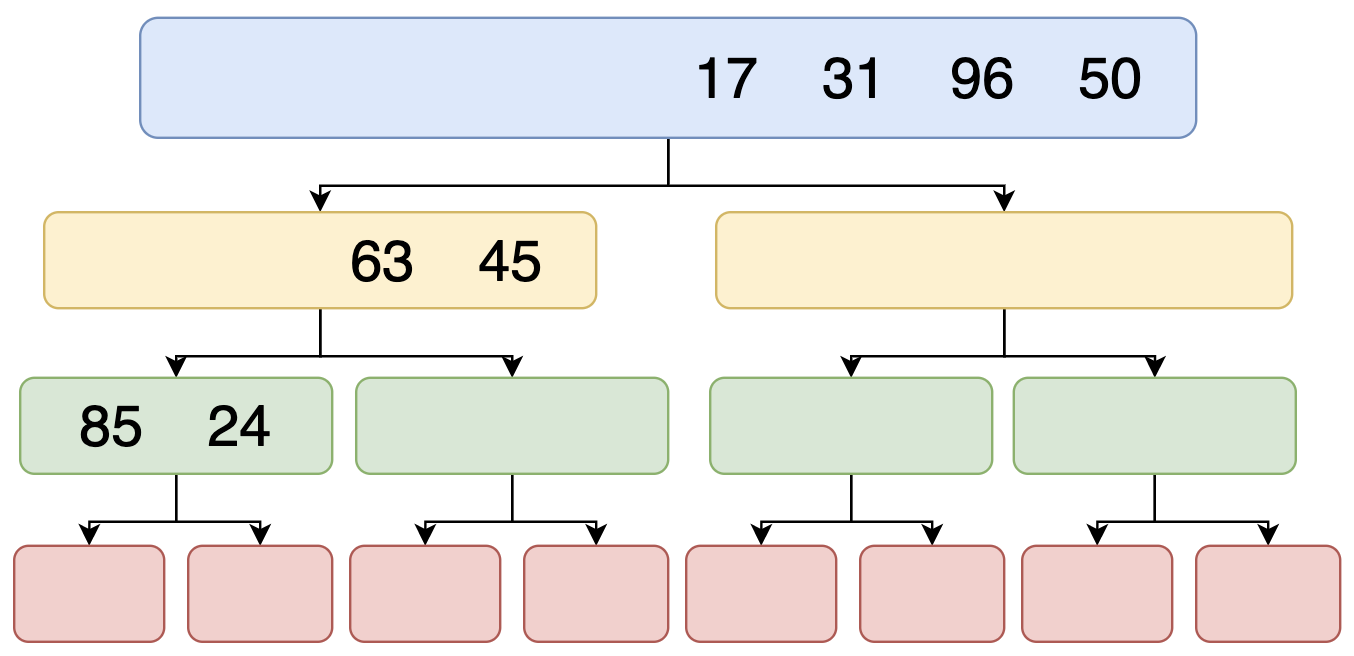
বাম পাশের Array টা আবার মাঝ বরাবর দুই ভাগে বিভক্ত করবে।

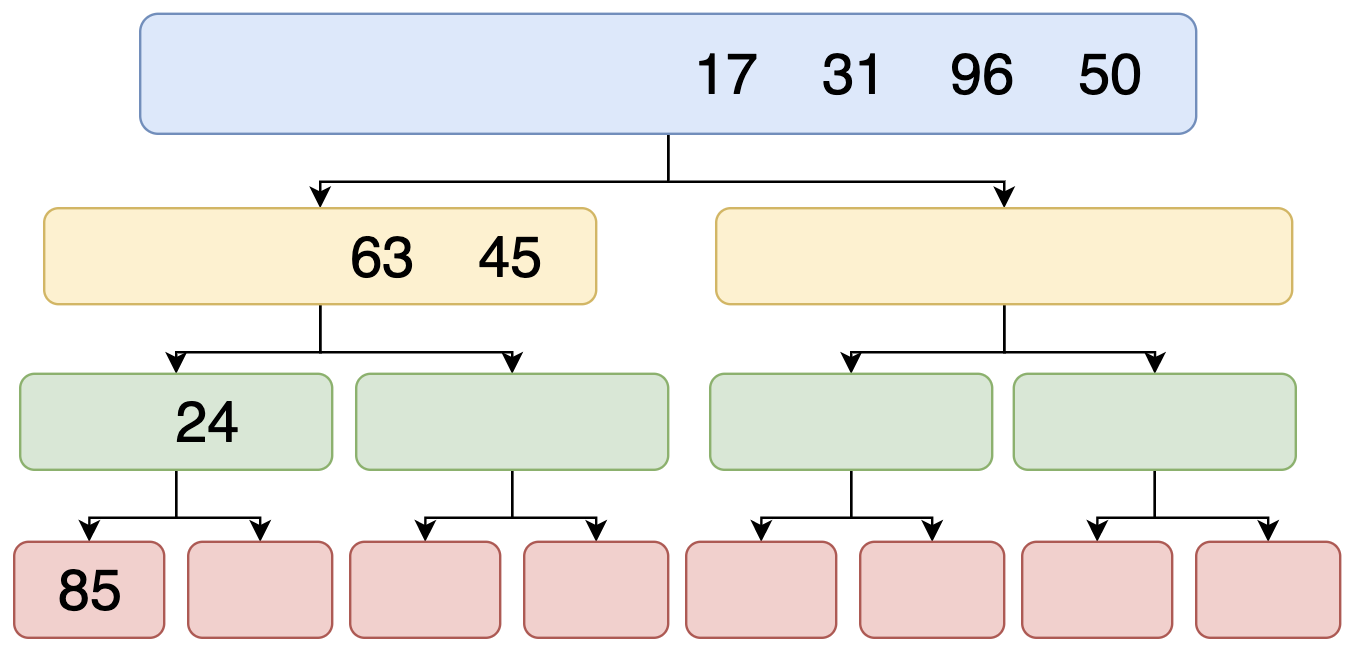
উপরের ছবির মত Array টা দুই ভাগে বিভক্ত হয়ে একটা এলিমেন্টে আসবে। এখন যেহেতু একটা এলিমেন্টে চলে আসছে আর একটা এলিমেন্ট কে ভাগ করা যায় না সুতরাং সে আবার রিটার্ন করবে। এবং পরের ডান দিকের কাজ শুরু হবে।

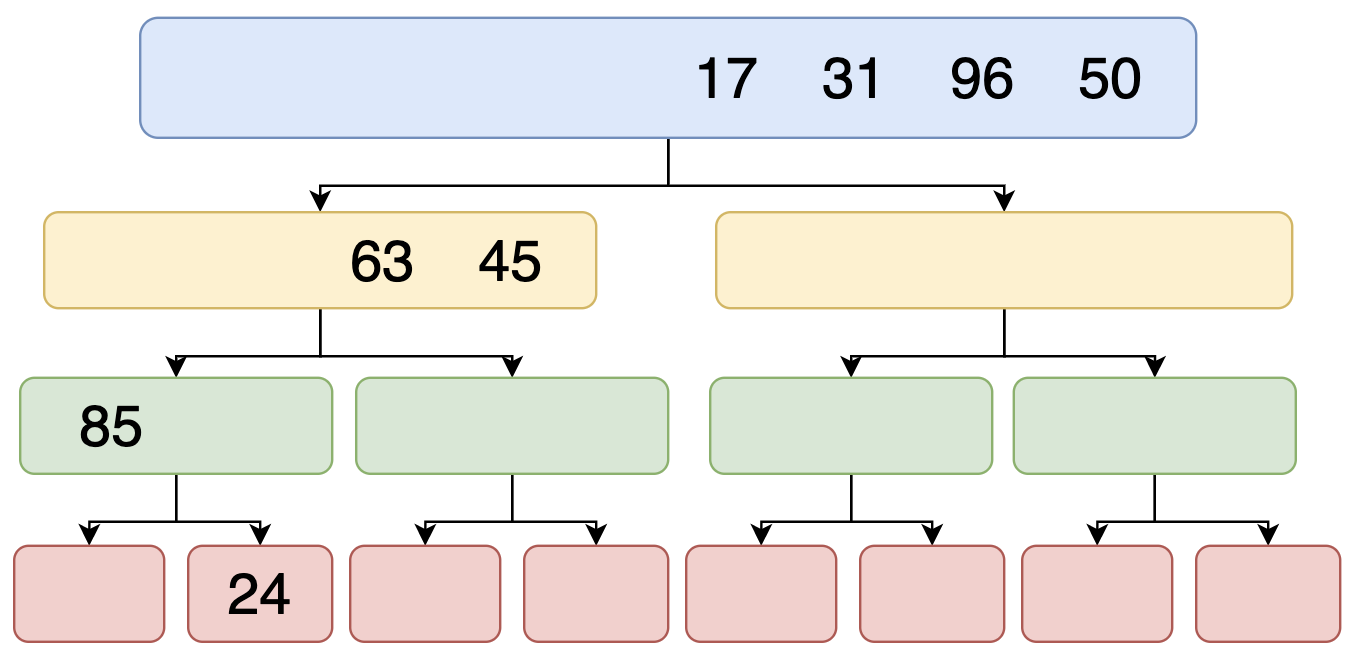
ডান পাশের এলিমেন্টেও যখন আর বিভক্ত করা যাবে না তখন সেও রিটার্ন করবে।

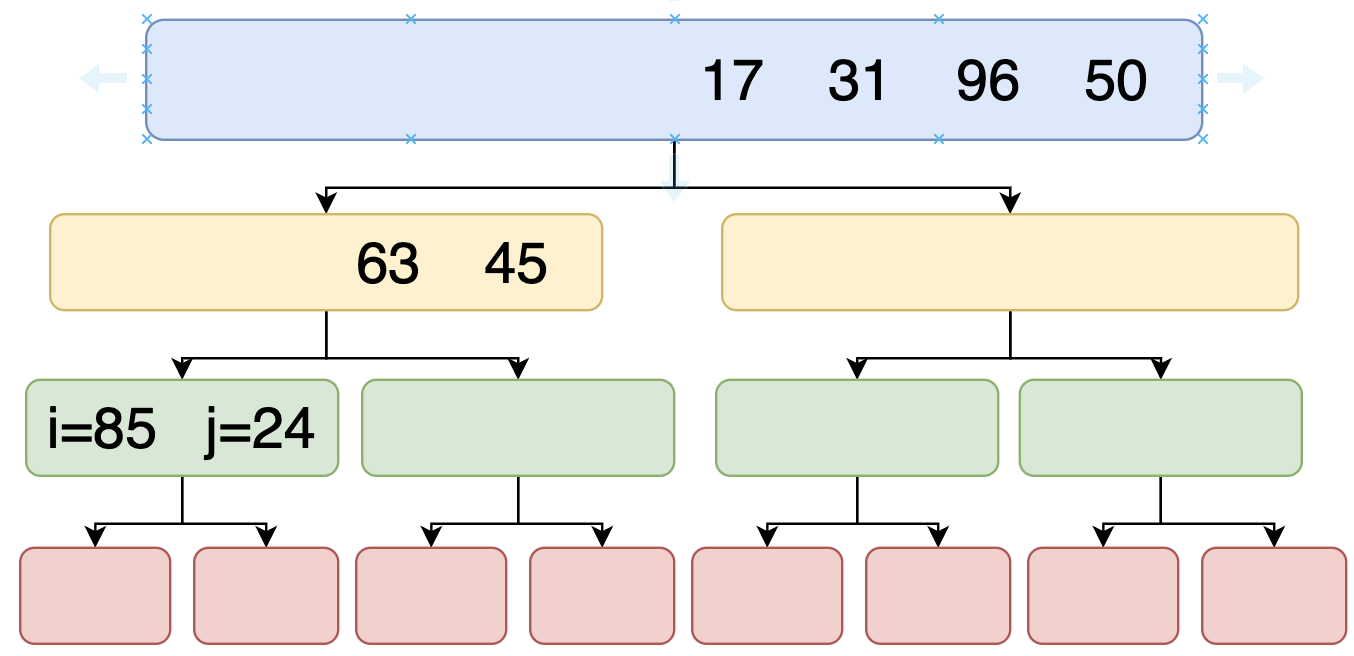
এখন আমরা 85 এবং 24 কে একটা Array চিন্তা করতে পারি। উপরে আমরা i এবং j এর মান ধরে চেক করা শিখেছিলাম। সেটাই এখানে প্রয়োগ করবো। যেহেতু আমরা Ascending Order এ সর্ট করছি তাই এদের মধ্যে জায়গা পরিবর্তন(swap) হবে এবং সেই Array টা রিটার্ন করবে।

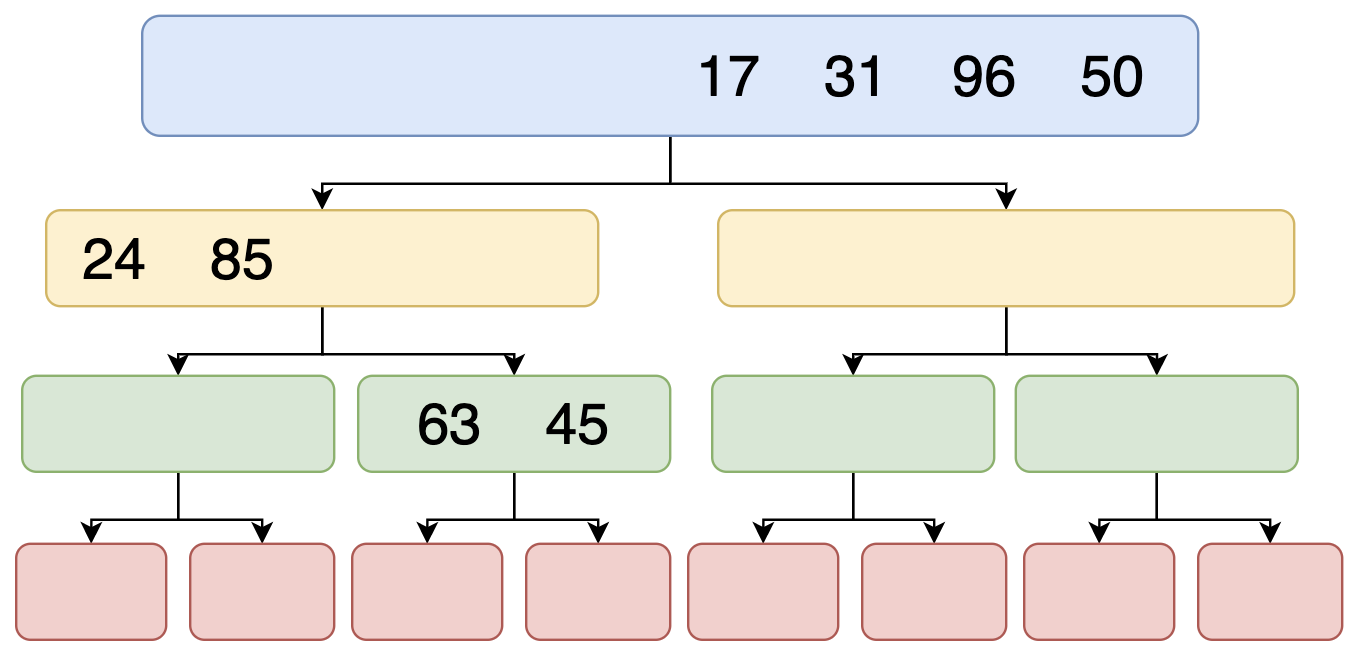
বাম পাশের কাজ যখন শেষ তখন ডান পাশের এলিমেন্ট গুলো দুই ভাগে বিভক্ত হবে এবং একটা এলিমেন্ট পর্যন্ত যাবে তারপর সে রিটার্ন করবে। পূর্বের মত সেও i এবং j এর ভ্যালু বসিয়ে চেক করবে। যেহেতু ডান পাশের এলিমেন্ট বড় তাই তাদের মধ্যে জায়গা পরিবর্তন(swap) হবে। নিচের ছবির মত

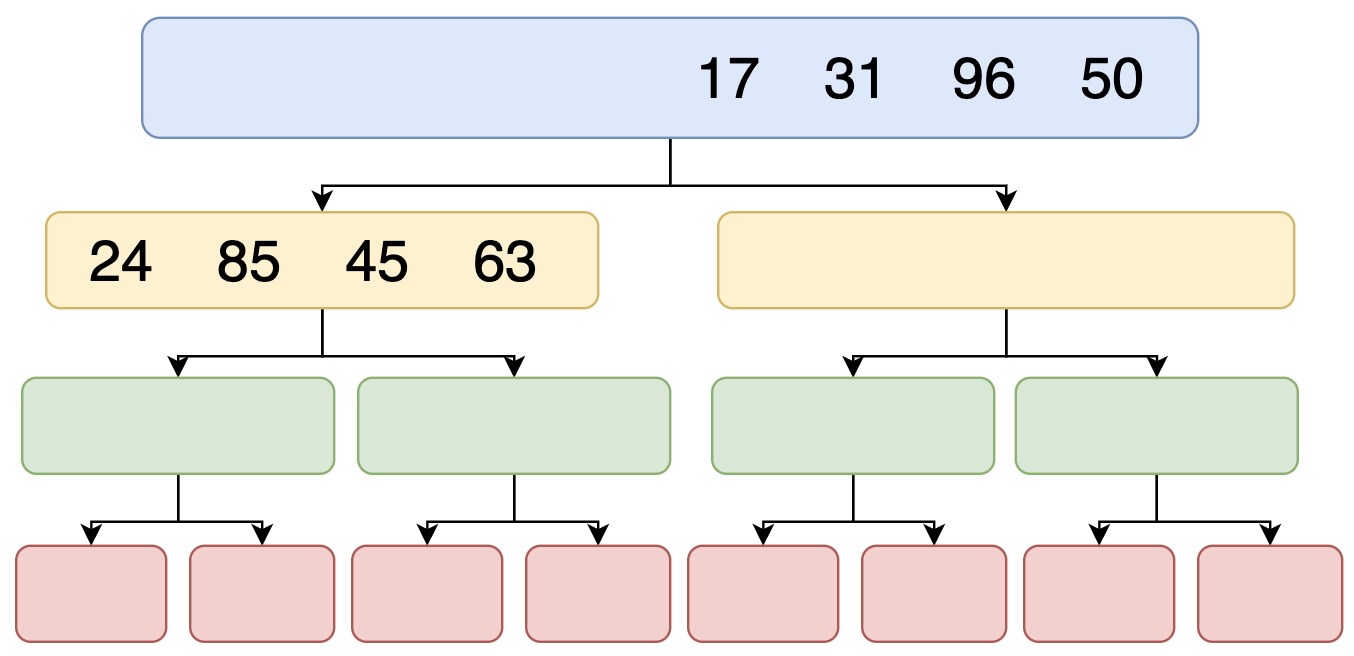
এখন খেয়াল করে দেখো 24 & 85 একটা Array আর 45 & 63 আরেক টা Array। দুটি Array কিন্তু Ascending Order এ সর্ট করা সুতরাং উপরের প্রোগ্রাম টা কাজে লাগাতে পারি। সে সর্টেড করে ভ্যালু রিটার্ন করবে।

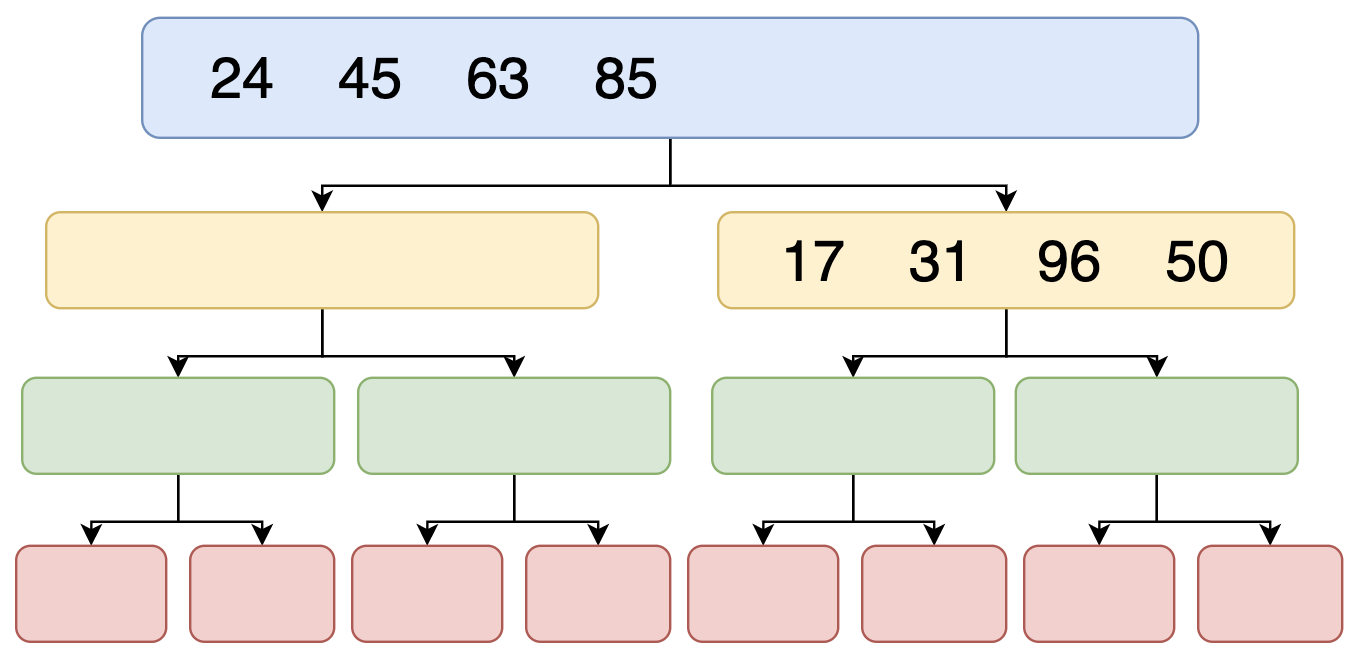
বাম পাশের কাজ শেষ হয়ে গেলে ডান পাশের কাজ শুরু করবে। বাম পাশের মত ডান পাশেও একইভাবে কাজ করবে এবং Ascending Order এ এলিমেন্ট গুলো সাজিয়ে ভ্যালু রিটার্ন করবে।

এখন দেখো বাম পাশের Array এবং ডান পাশের Array কিন্তু Ascending Order এ সর্টেড হয়ে গেছে সুতরাং আমরা উপরের প্রোগ্রাম টা ব্যবহার করে ফাইনাল রেজাল্ট পাবো।

এখন মার্জ সর্ট অ্যালগরিদমের টাইম কমপ্লেক্সিটি কত হবে? একটা ট্রি এর যত গুলো লেভেল থাকবে তার সাথে সব গুলা n এর গুণফল। ট্রি লেভেল বলতে কি বুঝায় বা ট্রি লেভেল কিভাবে বের করবো?
ডিসক্রিট ম্যাথে বলা আছে একটা বাইনারি ট্রি এর যদি n সংখ্যক নোড থাকে তাহলে তার টোটাল নাম্বার অফ লেভেল হবে logn সংখ্যাক। অবশ্যই বাইনারি ট্রি হতে হবে। যে ট্রি টা একটা প্যারেন্ট থেকে দুইটা চাইল্ড বের হতে পারে। এখানে টার্নারি ট্রি হবে না কারণ টার্নারি ট্রি তে ৩ টা চাইল্ড বের হয়। মার্জ সর্ট সব সময় বাইনারি ট্রি নিয়ে কাজ করে।

দুই টা করে যদি চাইল্ড বের হয় তাহলে সরবোচ্চ কতটা লেভেলের সংখ্যা হবে? উত্তর হচ্ছে logn সংখ্যক। এখন logn লেভেলের সাথে যদি n কে গুন করে দেই অর্থাৎ n*logn তাহলেই আমরা টাইম কমপ্লেক্সিটি পেয়ে যাচ্ছি O(nlogn)।
Best Case: O(nlogn)
Average Case: O(nlogn)
Worst Case: O(nlogn)

এটা হচ্ছে মার্জ সর্ট অ্যালগরিদম। আশা করি বুঝতে পারতেছো