মুশফিকুর রহমান নিলয়

বাবল সর্ট অ্যালগরিদম

সর্টিং অ্যালগরিদম গুলোর মধ্যে সব থেকে সহজ অ্যালগরিদম হলো বাবল সর্ট অ্যালগরিদম। আজকে আমরা বাবল সর্ট এর অ্যালগরিদম নিজ হাতে লিখবো, কোড করবো এবং বাবল সর্টের টাইম কমপ্লেক্সিটি বের করার চেষ্টা করবো। সুতরাং ধৈর্য নিয়ে পড়তে হবে।

বাবল সর্ট অ্যালগরিদম এর কাজ হচ্ছে পাশাপাশি দুইটা নোড থাকলে নোড দুইটার মধ্যে চেক করবে। এখানে নোড বলতে সংখ্যা কে বুঝানো হচ্ছে।
দুইটা নোডের মধ্যে কি চেক করবে? সেটা নির্ভর করবে আমরা ascending order এ সর্ট করতে যাচ্ছি নাকি descending order এ।
আমরা জানি ascending order মানে ছোট থেকে বড় আর descending order মানে বড় থেকে ছোট। যদি ছোট থেকে বড় আকারে সর্ট করতে চাই মানে ascending order এ তাহলে আমরা চেক করবো ডান পাশের সংখ্যা টা ছোট কিনা বাম পাশের সংখ্যার থেকে। আর descending order অর্থাৎ বড় থেকে ছোট আকারে সর্ট করতে চাইলে আমরা চেক করবো ডান পাশের সংখ্যা টা বড় কিনা বাম পাশের সংখ্যার থেকে।

একটু কঠিন মনে হচ্ছে? আচ্ছা সহজ করে বুঝিয়ে দিচ্ছি। মনে করো তোমাকে কিছু ছোট ছোট কাগজ দেওয়া হলো(নিচের ছবির মত)।

সেই কাগজে বিভিন্ন সংখ্যা লেখা আছে। যেমন ৩, ১, ৫, ৮ ইত্যাদি। তোমাকে বলা হলো কাগজের সংখ্যা গুলোকে ছোট থেকে বড় থেকে বড় আকারে সাজাও। তুমি প্রথমে একটা কাগজ নিয়ে দেখলে সেখানে ৫ লেখা আছে। সেই কাগজ টা এক দিকে রাখলে। তারপর আরেক টা কাগজ নিলে সেখানে ৮ লেখা আছে। সেই কাগজ টা নিশ্চয়ই ৫ এর ডান দিকে রাখবে কারণ তোমাকে বলা হয়েছে ছোট থেকে বড় আকারে সাজাতে। তারপর তুমি আরেক টা কাগজ নিলে, সেখানে ৩ লেখা আছে। এই কাগজ টা নিশ্চয়ই ৫ এর বাম পাশে রাখবে। কারণ ৩ সংখ্যা টা ৫ এর থেকে ছোট।
এতক্ষণ বাবল সর্ট অ্যালগরিদম কিভাবে কাজ করে তার একটা প্রাথমিক ধারনা পেয়েছ। এখন আমরা আরো ডিটেলসে দেখবো ।

উপরের ছবিতে কিছু এলোমেলো সংখ্যা নেওয়া হয়েছে। এই এলোমেলো সংখ্যা গুলো কে ছোট থেকে বড় আকারে সাজাতে হবে।
বাবল সর্ট অ্যালগরিদমের মাধ্যমে আমরা এই কাজটা করবো।

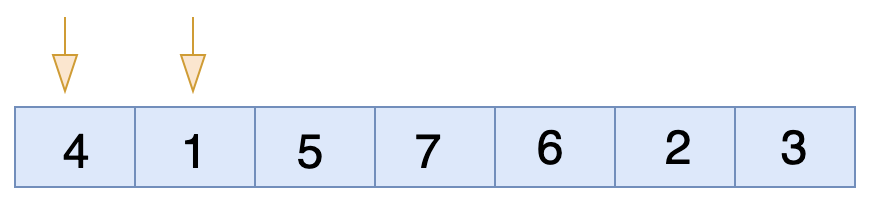
আগেই বলেছিলাম ২ টা নোড(সংখ্যার) মধ্যে চেক করবে। যেহেতু আমরা ascending order এ সর্ট করতে যাচ্ছি, তাই সে চেক করবে ডান দিকের সংখ্যা টা ছোট কিনা বাম দিকের সংখ্যার চেয়ে। যদি ডান দিকের সংখ্যা টা ছোট হয় তাহলে সংখ্যা ২ টির জায়গা পরিবর্তন(swap) করবে।
এখানে ডান পাশের সংখ্যা ১ আর বাম পাশের সংখ্যা ৪। যেহেতু ডান পাশের সংখ্যা ছোট ডান পাশের সংখ্যার থেকে তাই সংখ্যা ২ টির মধ্যে জায়গা পরিবর্তন(swap) হবে।

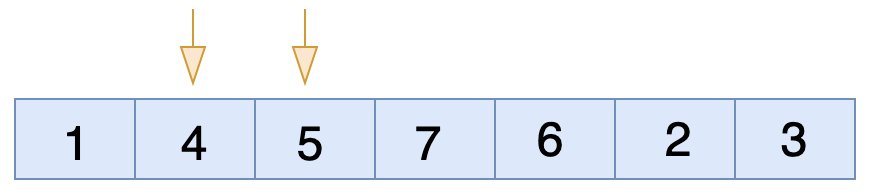
তার পরের ধাপে চেক করবে ৪ এবং ৫ এর মধ্যে। যেহেতু ডান পাশের সংখ্যাটা বড় বাম পাশের সংখ্যা টা থেকে অর্থাৎ কন্ডিশন মিথ্যা সুতরাং তাদের মধ্যে জায়গা পরিবর্তন(swap) হবে না।

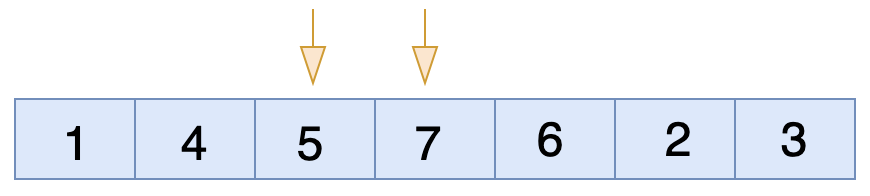
এখন ৫ এবং ৭ এর মধ্যে চেক করবে। এখানে কিন্তু ডান পাশের সংখ্যাটা বড় বাম পাশের সংখ্যা টা থেকে অর্থাৎ কন্ডিশন মিথ্যা সুতরাং তাদের মধ্যে জায়গা পরিবর্তন(swap) হবে না।

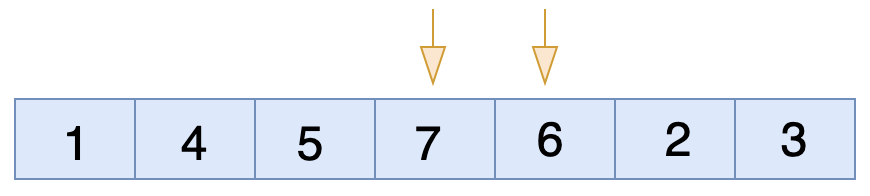
এখন ৭ এবং ৬ এর মধ্যে চেক করবে। এখানে কিন্তু ডান পাশের সংখ্যাটা ছোট বাম পাশের সংখ্যা টা থেকে অর্থাৎ কন্ডিশন সত্য সুতরাং তাদের মধ্যে জায়গা পরিবর্তন(swap) হবে।

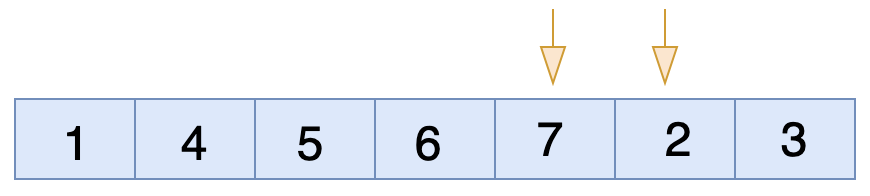
এখন ৭ এবং ২ এর মধ্যে চেক করবে। এখানেও ডান পাশের সংখ্যাটা ছোট বাম পাশের সংখ্যা টা থেকে অর্থাৎ কন্ডিশন সত্য সুতরাং তাদের মধ্যে জায়গা পরিবর্তন(swap) হবে।

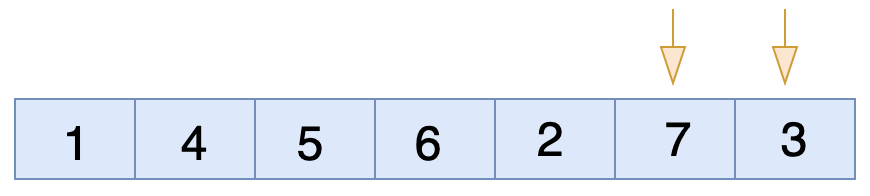
এখন ৭ এবং ৩ এর মধ্যে চেক করবে। এখানেও ডান পাশের সংখ্যাটা ছোট বাম পাশের সংখ্যা টা থেকে অর্থাৎ কন্ডিশন সত্য সুতরাং তাদের মধ্যে জায়গা পরিবর্তন(swap) হবে।

এখনও কিন্তু সব গুলো সংখ্যা সর্টেট অর্থাৎ ছোট থেকে বড় আকারে সাজানো হয়নি।
কিন্তু খেয়াল করে দেখো সব থেকে বড় সংখ্যা টা কিন্তু একদম ডান পাশে জায়গা করে নিয়েছে। সুতরাং পরের বার কিন্তু লাস্ট সংখ্যা টা চেক না করলে হবে।
আরেক টা বিষয় মনে রাখার জন্য তোমাদের কে বলছি, সেটা হলো আমরা সংখ্যা নিয়েছি ৭ টা কিন্তু চেক করেছি ৬ বার।

যেহেতু এখন পর্যন্ত সব গুলা সংখ্যা ছোট থেকে বড় আকারে সাজানো হয়নি তাই আবার চেক করতে হবে। অর্থাৎ যতক্ষণ পর্যন্ত সব গুলা সংখ্যা ছোট থেকে বড় আকারে সাজানো হবে না ততক্ষণ পর্যন্ত আমাদের কে উপরের কন্ডিশন মত চেক করতে হবে।

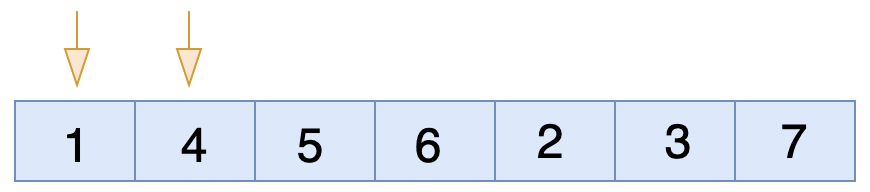
আবার ১ এবং ৪ এর মধ্যে চেক করবে। যেহেতু ডান পাশের সংখ্যা অর্থাৎ ৪ বড় আর বাম পাশের সংখ্যা অর্থাৎ ১ ছোট। সুতরাং কন্ডিশন মিথ্যা, তাই তাদের মধ্যে জায়গা পরিবর্তন(swap) হবে না।

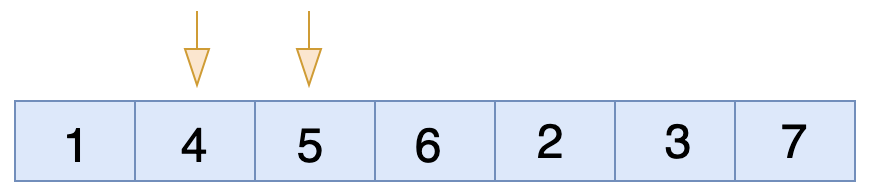
এখন ৪ এবং ৫ এর মধ্যে চেক করবে। যেহেতু ডান পাশের সংখ্যা অর্থাৎ ৫ বড় আর বাম পাশের সংখ্যা অর্থাৎ ৪ ছোট। সুতরাং কন্ডিশন মিথ্যা, তাই তাদের মধ্যে জায়গা পরিবর্তন(swap) হবে না।

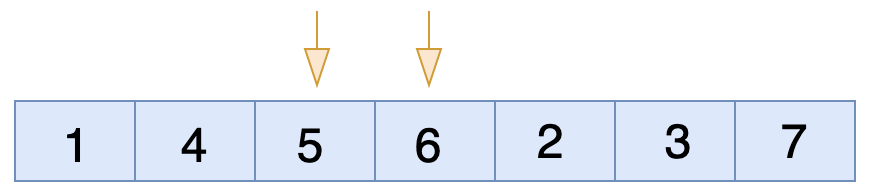
এখন ৫ এবং ৬ এর মধ্যে চেক করবে। যেহেতু ডান পাশের সংখ্যা অর্থাৎ ৬ বড় আর বাম পাশের সংখ্যা অর্থাৎ ৫ ছোট। সুতরাং কন্ডিশন মিথ্যা, তাই তাদের মধ্যে জায়গা পরিবর্তন(swap) হবে না।

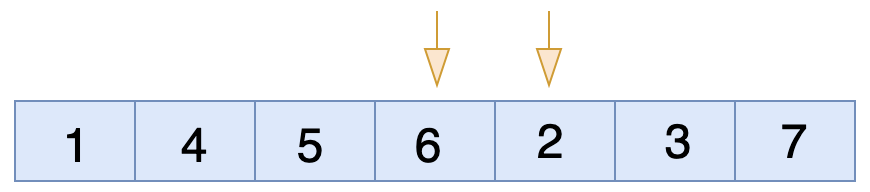
এখন ৬ এবং ২ এর মধ্যে চেক করবে। যেহেতু ডান পাশের সংখ্যা অর্থাৎ ২ ছোট আর বাম পাশের সংখ্যা অর্থাৎ ৬ বড় সুতরাং কন্ডিশন সত্য, তাই তাদের মধ্যে জায়গা পরিবর্তন(swap) হবে।

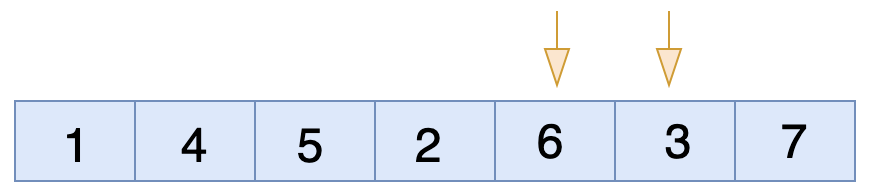
এখন ৬ এবং ৩ এর মধ্যে চেক করবে। যেহেতু ডান পাশের সংখ্যা অর্থাৎ ৩ ছোট আর বাম পাশের সংখ্যা অর্থাৎ ৬ বড় সুতরাং কন্ডিশন সত্য, তাই তাদের মধ্যে জায়গা পরিবর্তন(swap) হবে।

এখন ৬ এবং ৭ এর মধ্যে কিন্তু চেক করবে না। কারণ প্রথমবার যখন চেক করেছিলো তখনিই সব থেকে বড় সংখ্যা টা ডান পাশে চলে আসছিলো অর্থাৎ ৭ সংখ্যাটা। আর এবার সব থেকে বড় সংখ্যা ৬ কিন্তু ডান পাশে চলে আসছে এবং আগের বার ৬ বার চেক করেছিলো কিন্তু এখন ৫ বার চেক করা হয়েছে।
খেয়াল করে দেখো এখনও কিন্তু সব গুলা সংখ্যা ছোট থেকে বড় আকারে সাজানো হয়নি। সুতরাং আবার প্রথম থেকে চেক করতে হবে। যতক্ষণ পর্যন্ত সর্টেট না হবে ততক্ষণ পর্যন্ত চেক করতে হবে।

এভাবে চেক করতে থাকলে উপরের ছবির মত সর্টেট হয়ে যাবে।
বাবল সর্ট অ্যালগরিদম কিভাবে কাজ করে এটা আশা করি তোমরা বুঝতে পারছ।

এখন আমরা এর অ্যালগরিদম টা দেখবো

আমরা কিছু এলোমেলো সংখ্যা পাবো, সেই সংখ্যা গুলো কে A তে রাখা হয়েছে অর্থাৎ A হলো একটা Array।
Step 02 তে বলা হয়েছে A.length - 1 অর্থাৎ Array এর length যদি হয় ৭ তাহলে লুপটা ঘুরবে ৬ বার। তার কারণ উপড়ে তোমাদের কে বলে এসেছিলাম। তার পরের লুপে কিন্তু ৬ এবং ৭ এর মধ্যে চেক করিনি। এভাবে কমতে থাকে।
Step 03 তেও একই কাজ করা হয়েছে। Step 04 শুধু কন্ডিশন চেক করেছি। যদি ডান দিকের সংখ্যা টা ছোট হয় বাম দিকের সংখ্যা থেকে তাহলেই তাদের জায়গা পরিবর্তন(swap) হবে।

এখন উপরের অ্যালগরিদমের কোড দেখবো। আমি জাভাস্ক্রিপ্ট ব্যবহার করেছি, আপনি যেকোন ল্যাঙ্গুয়েজ ব্যবহার করতে পারেন।

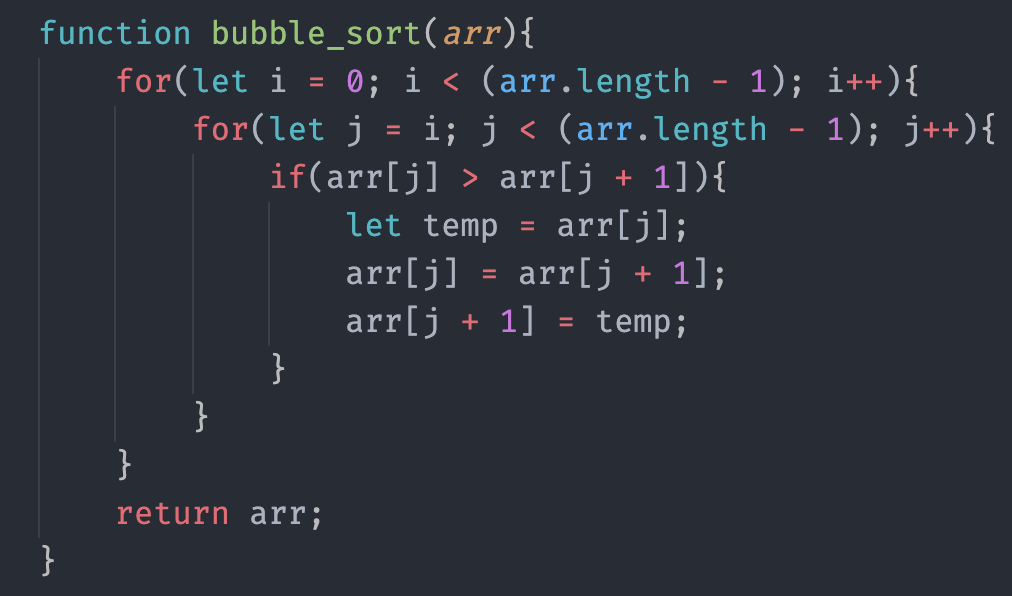
অ্যালগরিদম বুঝে থাকলে আশা করি কোড বুঝতে সমস্যা হবে না।
এখন এটার টাইম কমপ্লেক্সিটি কি হবে? Worst Case & Avarage Case এর জন্য হবে O(n2)